
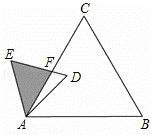
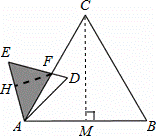
如图,已知△ABC是面积为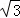 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号)
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号) .
.
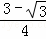
考点:相似三角形的性质;等边三角形的性质.
专题:计算题.
分析:根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,再根据求出其边长,可根据三角函数得出三角形面积.
解答: 解:∵△ABC∽△ADE,AB=2AD,
∴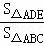 =
=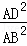 ,
,
∵AB=2AD,S△ABC=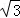 ,
,
∴S△ADE=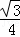 ,
,
如图,在△EAF中,过点F作FH⊥AE交AE于H,
∵∠EAF=∠BAD=45°,∠AEF=60°,
∴∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°=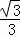 x.
x.
又∵S△ADE=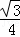 ,
,
作CM⊥AB交AB于M,
∵△ABC是面积为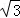 的等边三角形,
的等边三角形,
∴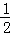 ×AB×CM=
×AB×CM=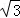 ,
,
∠BCM=30°,
设AB=2k,BM=k,CM=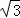 k,
k,
∴k=1,AB=2,
∴AE=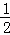 AB=1,
AB=1,
∴x+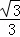 x=1,
x=1,
解得x=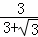 =
=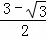 .
.
∴S△AEF=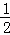 ×1×
×1×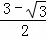 =
= .
.
故答案为: .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,∠A=70°.⊙O截△ABC的三条边 所得的弦长相等,则∠BOC的度数为( )
所得的弦长相等,则∠BOC的度数为( )
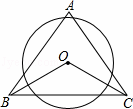
A.160° B.135° C.125° D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
对于实数a、b,定义运算“*”:a*b=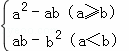 ,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.
,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.
查看答案和解析>>
科目:初中数学 来源: 题型:
.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是10平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
某商店的一种服装,每件成本为50元,经市场调研,售价为60元时,可销售800件,售价每提高2元,销量将减少40件,已知商店销售这批服装获利12000元,问这种服装每件售价是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com