
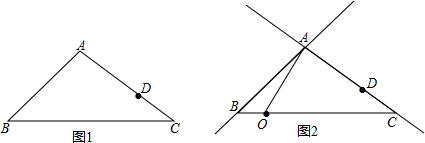
���� ��1������A��AG��BC��G���õ���AGB=��AGC=90�㣬��Rt��ABG�У����ڡ�ABG=��BAG=45�㣬�õ�BG=AG����Rt��ACG�У��������Ǻ�����ý����
��2���ٵ�CB=CD=5ʱ����CBDΪ���������Σ��ڵ�BD=DCʱ������D��DH��BC��H���õ�CH=$\frac{1}{2}$BC=$\frac{5}{2}$���ɡ�ACB������ֵ��ã��۵�BC=BDʱ������B��BM��CD��M���õ�CM=$\frac{1}{2}$CD����tan$��ACB=\frac{BM}{CM}$=$\frac{3}{4}$���з�����ý����
��3�����ڣ��Ե�E��D��O��AΪ������ı�����ƽ���ı����������������Σ��ٵ��ı���AE1OD1Ϊƽ���ı���ʱ��$\frac{BE}{CD}$=$\frac{3\sqrt{2}}{20}$���ڵ��ı���AD2E1OΪƽ���ı���ʱ��$\frac{BE}{CD}$=$\frac{\sqrt{2}}{10}$���۵��ı���AOD1E2Ϊƽ���ı���ʱ��$\frac{BE}{CD}$=$\frac{27\sqrt{2}}{20}$��
��� 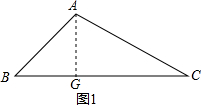 �⣺��1������A��AG��BC��G��
�⣺��1������A��AG��BC��G��
���AGB=��AGC=90�㣬
��Rt��ABG�У��ߡ�ABG=��BAG=45�㣬
��BG=AG��
��Rt��ACG��
��tan��acb=$\frac{AG}{GC}$=$\frac{3}{4}$��
��AG=3x����CG=4x��BG=3x��
��BC+=BG+CG=5�ã�
x=$\frac{5}{7}$��
��BG=AG=$\frac{15}{7}$��CG=$\frac{20}{7}$��
��AB=$\frac{15\sqrt{2}}{7}$��AC=$\frac{25}{7}$��
��2���ٵ�CB=CD=5ʱ����CBDΪ���������Σ�
�ڵ�BD=DCʱ����ͼ2������D��DH��BC��H��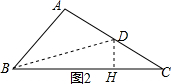
��CH=$\frac{1}{2}$BC=$\frac{5}{2}$��
��tan��ACB=$\frac{DH}{CH}$=$\frac{3}{4}$��
��DH=$\frac{15}{8}$��
��CD=$\frac{25}{8}$��
�۵�BC=BDʱ����ͼ3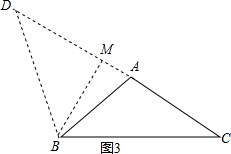
����B��BM��CD��M��
��CM=$\frac{1}{2}$CD��
��tan$��ACB=\frac{BM}{CM}$=$\frac{3}{4}$��
��BM=3t��CM=4t����BC=5t=5��
��t=1��
��CM=4t=4��
��CD=8��
��3�����ڣ���3�����ڣ��Ե�E��D��O��AΪ������ı�����ƽ���ı����������������Σ�
�ٵ��ı���AE1OD1Ϊƽ���ı���ʱ��$\frac{BE}{CD}$=$\frac{3\sqrt{2}}{20}$��
�ڵ��ı���AD2E1OΪƽ���ı���ʱ��$\frac{BE}{CD}$=$\frac{\sqrt{2}}{10}$��
�۵��ı���AOD1E2Ϊƽ���ı���ʱ��$\frac{BE}{CD}$=$\frac{27\sqrt{2}}{20}$��
���� ���⿼����Ƕ�Ԫһ�η������Ӧ�ã����������ε��ж������ʣ�������Ǻ�����ƽ���ı��ε��ж��Լ��߶αȵ��й�֪ʶ��ע���������˼���Ӧ�ò�Ҫ©�⣮


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͼ���㣨2��2�� | B�� | y��x���������С | ||
| C�� | ͼ��λ�ڵ�һ�������� | D�� | ��x��1ʱ��y��ֵ������2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��1�� | 2 |
| ��2�� | 4 6 |
| ��3�� | 8 10 12 14 |
| �� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����ijУ���꼶���40��ѧ������Ҫ�μ���������ѡһ����ѡ��Ŀ���ԣ���ͼ�Ǹð�ѧ��������ѡ��Ŀ����������ͳ��ͼ�������ͼ����Ϣ�����������⣺
�����ijУ���꼶���40��ѧ������Ҫ�μ���������ѡһ����ѡ��Ŀ���ԣ���ͼ�Ǹð�ѧ��������ѡ��Ŀ����������ͳ��ͼ�������ͼ����Ϣ�����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
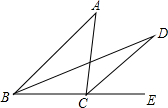 ��ͼ����֪��ABC�У���ABC��ƽ�������ACE��ƽ���߽��ڵ�D������A=50�㣬���D=25�ȣ�
��ͼ����֪��ABC�У���ABC��ƽ�������ACE��ƽ���߽��ڵ�D������A=50�㣬���D=25�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | -$\frac{2}{3}$ | C�� | $\frac{3}{2}$ | D�� | -$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com