
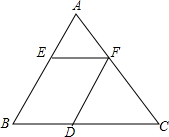
 如图,△ABC中,EF∥BC,FD∥AB,AE=12,BE=18,AF=14,CD=24,求线段FC,EF的长.
如图,△ABC中,EF∥BC,FD∥AB,AE=12,BE=18,AF=14,CD=24,求线段FC,EF的长. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在一场足球赛中,一球员从球门正前方10m处将球踢起射向球门,当球飞行的水平距离是6m时,球达到最高点,此时球高3m,将球的运行路线看成是一条抛物线,若球门高为2.44m,则该球员能射中球门(填“能”或“不能”).
如图所示,在一场足球赛中,一球员从球门正前方10m处将球踢起射向球门,当球飞行的水平距离是6m时,球达到最高点,此时球高3m,将球的运行路线看成是一条抛物线,若球门高为2.44m,则该球员能射中球门(填“能”或“不能”).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.
如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com