
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )
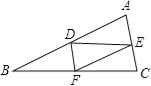
A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
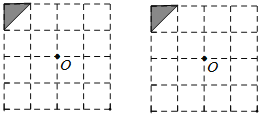
【题目】(1)如图是一个4×4的正方形网格,每个小正方形的边长均为1.请在网格中以左上角的三角形为基本图形,通过平移、对称或旋转,设计两个精美图案,使其满足:①既是轴对称图形,又能以点![]() 为旋转中心旋转而得到;②所作图案用阴影标识,且阴影部分面积为4.
为旋转中心旋转而得到;②所作图案用阴影标识,且阴影部分面积为4.
(2)如图,![]() 的三个顶点和点
的三个顶点和点![]() 都在正方形网格的格点上,每个小正方形的边长都为1.
都在正方形网格的格点上,每个小正方形的边长都为1.
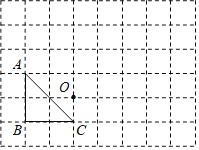
①将![]() 先向右平移4个单位,再向上平移2个单位得到
先向右平移4个单位,再向上平移2个单位得到![]() ,请画出
,请画出![]() ;
;
②请画出![]() ,使
,使![]() 和
和![]() 关于点
关于点![]() 成中心对称;
成中心对称;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA的延长线与OC的延长线于点E,F,连接BF.

(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(a,a),点B的坐标(b,c),且a、b、c满足![]() .
.
(1)若a没有平方根,判断点A在第几象限并说明理由.
(2)连AB、OA、OB,若△OAB的面积大于5而小于8,求a的取值范围;
(3)若两个动点M(2m,3m-5),N(n-1,-2n-3),请你探索是否存在以两个动点M、N为端点的线段MN∥AB,且MN=AB.若存在,求出M、N两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
查看答案和解析>>
科目:初中数学 来源: 题型:
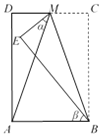
【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享经济来临,某企业决定在无锡投入共享单车(自行车)和共享电单车(电动车)共2000辆,已知每辆共享单车成本380元,每台共享电单车成本1500元,2辆共享单车和1辆共享电单车每周毛利31元,4辆共享单车和3辆共享电单车每周毛利81元,
(1)求共享单车和共享电单车每周每辆分别可以盈利多少元?
(2)为考虑投资回报率,该企业计划投入成本不超过174万元,每周的毛利不低于23050元,现要求投入的单车数量为10的倍数,请你列举出所有投入资金方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com