
 一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$.
一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$. 分析 先将图形展开,再根据两点之间线段最短,再由勾股定理求解即可.
解答 解:如图1:
AB=$\sqrt{1{6}^{2}+{3}^{2}}$=$\sqrt{265}$(cm),
如图2:
AB=$\sqrt{1{5}^{2}+{4}^{2}}$=$\sqrt{241}$(cm),
如图3:
AB=$\sqrt{1{2}^{2}+{7}^{2}}$=$\sqrt{193}$(cm),
∴$\sqrt{265}$>$\sqrt{241}$>$\sqrt{193}$,
∴它所行的最短路线的长是$\sqrt{193}$cm.
故答案为:$\sqrt{193}$cm.
点评 本题考查的是平面展开-最短路径问题,熟知两点之间线段最短是解答此题的关键.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
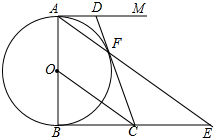 如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.
如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com