
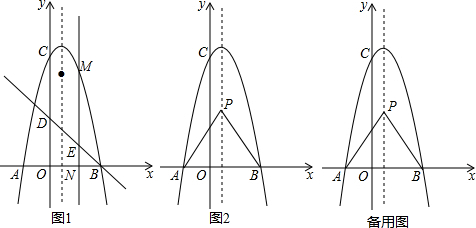
分析 (1)把点B代入以及利用对称轴公式列出方程组解决.
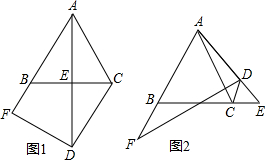
(2)如图1中,作MF⊥BD垂足为F,设M(m,-m2+2m+8),因为∠MED=∠BEN,∠MFE=∠ENB=90°由△MFE∽△BNE得$\frac{NF}{BN}=\frac{ME}{EB}$=2$\sqrt{2}$,列出方程解决.
(3)分三种情形列出方程解决,①如图2中,当点Q在点P上方,设Q(1,m),根据S△BQQ′=S△PQQ′+S△PBQ′-S△PBQ=$\frac{\sqrt{3}}{4}$列出方程即可解决,②如图3中当点Q在点P下方,设Q(1,m)(m<$\sqrt{3}$),根据S△BQQ′=S△PQB+S△PQQ′-S△PBQ′=$\frac{\sqrt{3}}{4}$列出方程即可解决.③如图4中,当点Q在点P下方,设Q(1,m)($\sqrt{3}$<m<3$\sqrt{3}$),根据S△BQQ′=S△PBQ′-S△PQQ′-S△PQB=$\frac{\sqrt{3}}{4}$列出方程即可解决.
解答 解:(1)∵直线y=-x+4与x轴交于点B,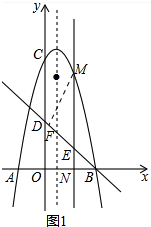
∴点B坐标(4,0),由题意$\left\{\begin{array}{l}{16a+4b+8=0}\\{-\frac{b}{2a}=1}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+8.
(2)如图1中,作MF⊥BD垂足为F,设M(m,-m2+2m+8),
∵∠MED=∠BEN,∠MFE=∠ENB=90°,
∴△MFE∽△BNE,
∴$\frac{NF}{BN}=\frac{ME}{EB}$=2$\sqrt{2}$,
∴ME=2$\sqrt{2}$EB,
∵OD=OB=4,∠DOB=90°,
∴∠ODB=45°,EB=$\sqrt{2}$BN,
∴ME=4BN,
∴-m2+2m+8-(-m+4)=4(4-m)
∴m=3(或4不合题意舍弃),
∴点M坐标为(3,5)
(3)存在.
①如图2中,当点Q在点P上方,设Q(1,m),∵△PQQ′、△PAB是等边三角形,
∴QP=PQ′=m-3$\sqrt{3}$,∠BPQ′=90°,
∴S△BQQ′=S△PQQ′+S△PBQ′-S△PBQ=$\frac{\sqrt{3}}{4}$,
∴$\frac{1}{2}$×$6×(m-3\sqrt{3}$)+×$\frac{\sqrt{3}}{4}$(m-3$\sqrt{3}$)2-$\frac{1}{2}×3×$(m-3$\sqrt{3}$),
整理得$\sqrt{3}$(m-3$\sqrt{3}$)2+6(m-3$\sqrt{3}$)-$\sqrt{3}$=0,
解得m=2$\sqrt{3}$+2(或2$\sqrt{3}$-2不合题意舍弃),此时PQ=2-$\sqrt{3}$
②如图3中,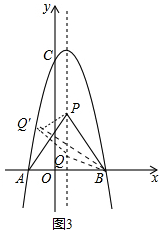 当点Q在点P下方,设Q(1,m)(m<$\sqrt{3}$),
当点Q在点P下方,设Q(1,m)(m<$\sqrt{3}$),
∵△PQQ′、△PAB是等边三角形,
∴QP=PQ′=3$\sqrt{3}$-m,∠BPQ′=90°,
∴S△BQQ′=S△PQB+S△PQQ′-S△PBQ′=$\frac{\sqrt{3}}{4}$,
∴$\frac{1}{2}$×$(3\sqrt{3}-m)$×3+$\frac{\sqrt{3}}{4}$(3$\sqrt{3}$-m)2-$\frac{1}{2}$×6×(3$\sqrt{3}$-m)=$\frac{\sqrt{3}}{4}$,
整理得$\sqrt{3}$(3$\sqrt{3}$-m)2-6(3$\sqrt{3}$-m)-$\sqrt{3}$=0
解得m=2$\sqrt{3}$-2(或2$\sqrt{3}$+2不合题意舍弃),此时PQ=$\sqrt{3}+2$
③如图4中,当点Q在点P下方,设Q(1,m)($\sqrt{3}$<m<3$\sqrt{3}$),
∵△PQQ′、△PAB是等边三角形,
∴QP=PQ′=3$\sqrt{3}$-m,∠BPQ′=90°,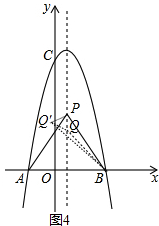 ∴S△BQQ′=S△PBQ′-S△PQQ′-S△PQB=$\frac{\sqrt{3}}{4}$,
∴S△BQQ′=S△PBQ′-S△PQQ′-S△PQB=$\frac{\sqrt{3}}{4}$,
∴$\frac{1}{2}$×$6×(3\sqrt{3}-m)$-$\frac{\sqrt{3}}{4}$(3$\sqrt{3}$-m)2-$\frac{1}{2}$×(3$\sqrt{3}$-m)×3=$\frac{\sqrt{3}}{4}$,
整理得$\sqrt{3}$(3$\sqrt{3}$-m)2-6(3$\sqrt{3}$-m)+$\sqrt{3}$=0
解得m=2$\sqrt{3}$$±\sqrt{2}$.
此时PQ=$\sqrt{3}$$±\sqrt{2}$,
综上所述:PQ的长为2$±\sqrt{3}$或$\sqrt{3}$±$\sqrt{2}$.
点评 本题考查二次函数的解析式的求法、三角形的面积、旋转的性质、等边三角形的性质等知识,解题的关键是用方程的思想去思考问题,需要正确画出图形,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,
如图,在平面直角坐标系中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
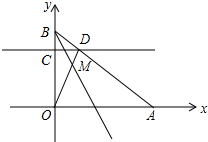 已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD.
已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
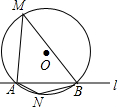 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com