
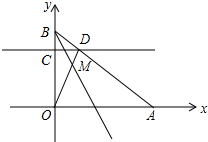
 已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD.
已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD.分析 ①根据非负数的性质得出A、B的坐标,然后根据待定系数法即可求得直线AB的解析式,根据C的坐标得出D的纵坐标,代入解析式即可求得横坐标;
拓展:根据D的坐标求得OD的解析式,根据D的纵坐标和PQ=$\frac{1}{2}$,求得Q的纵坐标,代入解析式求得横坐标,然后根据三角形面积公式即可求得;
②根据平行线的性质得出∠BCD=90°,∠CDO=∠AOD,根据∠AOD=∠ADO得出∠ADC=90°+∠OBD=2∠AOD,由∠OBD=2∠MBO,得出2∠AOD=90°+2∠MBO,得出∠AOD=45°+∠MBO,由∠AOD=90°-∠MOB,得出∠MOB+∠MBO=45°;
③作EP⊥x轴于P,DQ⊥x轴于Q,根据S△EOD=S梯形EPQD-S△OPE-S△OPQ得出S△EOD=$\frac{1}{3}$|y|+$\frac{15}{6}$,
由S△ODE>4S△AOD得出$\frac{1}{3}$|y|+$\frac{15}{6}$>4×5,解不等式即可求得.
解答 解:∵平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,
∴a=4,b=3,
∴A(4,0),B(0,3),
设直线AB的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{4m+n=0}\\{n=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=-\frac{3}{4}}\\{n=3}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{3}{4}$x+3,
①∵CD∥x轴,C(0,$\frac{5}{2}$),
∴D的纵坐标为$\frac{5}{2}$,
∴$\frac{5}{2}$=-$\frac{3}{4}$x+3,解得x=$\frac{2}{3}$,
∴D($\frac{2}{3}$,$\frac{5}{2}$);
拓展:∵D($\frac{2}{3}$,$\frac{5}{2}$),
∴直线OD:y=$\frac{15}{4}$x,
当Q点在线段OD上时,
∵P的纵坐标为$\frac{5}{2}$,PQ=$\frac{1}{2}$,
∴Q的纵坐标为2,
代入y=$\frac{15}{4}$x得,2=$\frac{15}{4}$x,解得x=$\frac{8}{15}$,
∴Q($\frac{8}{15}$,2);
∴S△OCQ=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{8}{15}$=$\frac{2}{3}$,
当Q点在线段AB上时,∵P的纵坐标为$\frac{5}{2}$,PQ=$\frac{1}{2}$,
∴Q的纵坐标为2,
代入y=-$\frac{3}{4}$x+3得,2=-$\frac{3}{4}$x+3,解得x=$\frac{4}{3}$,
∴Q($\frac{4}{3}$,2);
∴S△OCQ=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{4}{3}$=$\frac{5}{3}$,
故△OCQ的面积为$\frac{2}{3}$或$\frac{5}{3}$;
②∵CD∥OA,
∴∠BCD=90°,∠CDO=∠AOD,
∵∠AOD=∠ADO
∴∠ADC=90°+∠OBD=2∠AOD,
∵∠OBD=2∠MBO,
∴2∠AOD=90°+2∠MBO,
∴∠AOD=45°+∠MBO,
∵∠AOD=90°-∠MOB,
∴∠MOB+∠MBO=45°;
拓展:∵AN∥OD,
∴∠ANB=∠BMD,
∵∠BMD=∠MOB+∠MBO=45°,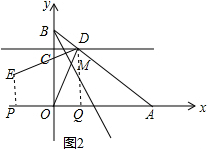
∴∠ANB=45°;
③作EP⊥x轴于P,DQ⊥x轴于Q,
∵A(4,0),D($\frac{2}{3}$,$\frac{5}{2}$),E(-2,y),
∴S△AOD=$\frac{1}{2}$×4×$\frac{5}{2}$=5,
∵S△EOD=S梯形EPQD-S△OPE-S△OPQ
=$\frac{1}{2}$(|y|+$\frac{5}{2}$)(2+$\frac{2}{3}$)-$\frac{1}{2}×$2×|y|-$\frac{1}{2}$×$\frac{2}{3}$×$\frac{5}{2}$
=$\frac{1}{3}$|y|+$\frac{15}{6}$,
∵S△ODE>4S△AOD,
∴$\frac{1}{3}$|y|+$\frac{15}{6}$>4×5,
解得|y|>$\frac{105}{2}$,
∴y>$\frac{105}{2}$或y<-$\frac{105}{2}$.
点评 本题考查了坐标和图形的性质,平行线的性质,待定系数法求一次函数的解析式,三角形的面积等,③作出辅助线根据直角梯形是关键.


科目:初中数学 来源: 题型:解答题
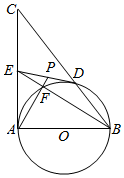 如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
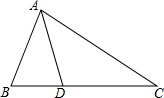 如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.
如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com