Question

4．有一座桥，桥孔的形状是一条开口向下的抛物线y=-$\frac{1}{2}$x²
（1）画出桥孔抛物草图；
（2）利用图象求：当水平线离开抛物线顶点2米时，水面的宽是多少米？
（3）利用图象求：当水面宽为6米时，水平线离顶点的距离为多少米？（精确到0.1米）
（4）利用对称性的知识理解2）、3）两问的解法．

Answer 1

分析 （1）由二次函数的性质可知抛物线开口向下，对称轴为y轴，顶点坐标为（0，0）；
（2）将y=-2代入解析式求得x的值，从而可求得水面的宽；
（3）由抛物线的对称性可知：x₁=-3，x₂=3，将x₁=-3或x₂=3代入解析式可求得y值；
（4）依据抛物线的对称性回答即可．

解答 解：（1）函数图象如图所示：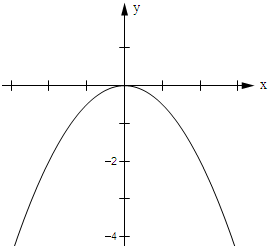

（2）将y=-2代入解析式得：-$\frac{1}{2}$x²=-2，
解得：x₁=-2，x₂=2．
故水面的宽度=2-（-2）=4米．
（3）由抛物线的对称性可知：x₁=-3，x₂=3．
将x=3代入得：y=-$\frac{1}{2}×{3}^{2}$=-4.5米．
（4）根据抛物线的对称性可知：当x₁=-2和x₂=2时，两点的纵坐标相同；当x₁=-3和x₂=3两点的纵坐标相同．

点评 本题主要考查的是二次函数的图象和性质，掌握抛物线的对称性是解题的关键．