
【题目】如图1,四边形ABCD中,BD⊥AD,E为BD上一点,AE=BC,CE⊥BD,CE=ED

(1)已知AB=10,AD=6,求CD;
(2)如图2,F为AD上一点,AF=DE,连接BF,交BF交AE于G,过G作GH⊥AB于H,∠BGH=75°.求证:BF=2![]() GH+
GH+![]() EG.
EG.
【答案】(1)2![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)由勾股定理得出BD=![]() =8,由HL证得Rt△ADE≌Rt△BEC,得出BE=AD,则CE=ED=BD﹣BE=BD﹣AD=2,由等腰直角三角形的性质即可得出结果;
=8,由HL证得Rt△ADE≌Rt△BEC,得出BE=AD,则CE=ED=BD﹣BE=BD﹣AD=2,由等腰直角三角形的性质即可得出结果;
(2)连接CF,易证AF=CE,AD∥CE,得出四边形AECF是平行四边形,则AE=CF,AE∥CF,得出∠CFD=∠EAD,∠CFB=∠AGF,由Rt△ADE≌Rt△BEC,得出∠CBE=∠EAD,推出∠CBE=∠CFD,证得△BCF是等腰直角三角形,则BF=![]() BC=
BC=![]() CF=
CF=![]() AE,∠FBC=∠BFC=45°,推出∠AGF=45°,∠AGH=60°,∠GAH=30°,则AG=2GH,得出BF=
AE,∠FBC=∠BFC=45°,推出∠AGF=45°,∠AGH=60°,∠GAH=30°,则AG=2GH,得出BF=![]() AE=
AE=![]() (AG+EG),即可得出结论.
(AG+EG),即可得出结论.
(1)解:∵BD⊥AD,
∴BD=![]() =
=![]() =8,
=8,
∵CE⊥BD,
∴∠CEB=∠EDA=90°,
在Rt△ADE和Rt△BEC中,![]() ,
,
∴Rt△ADE≌Rt△BEC(HL),
∴BE=AD,
∴CE=ED=BD﹣BE=BD﹣AD=8﹣6=2,
∴CD![]() =CE=2
=CE=2![]() ;
;
(2)解:连接CF,如图2所示:
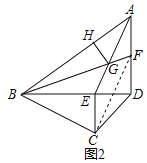
∵AF=DE,DE=CE,
∴AF=CE,
∵BD⊥AD,CE⊥BD,
∴AD∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,AE∥CF,
∴∠CFD=∠EAD,∠CFB=∠AGF,
由(1)得:Rt△ADE≌Rt△BEC,
∴∠CBE=∠EAD,
∴∠CBE=∠CFD,
∵∠FBD+∠BFC+∠CFD=90°,
∴∠FBD+∠BFC+∠CBE=90°,
∴∠BCF=90°,
∵AE=BC,
∴BC=CF,
∴△BCF是等腰直角三角形,
∴BF=![]() BC=
BC=![]() CF=
CF=![]() AE,∠FBC=∠BFC=45°,
AE,∠FBC=∠BFC=45°,
∴∠AGF=45°,
∵∠BGH=75°,
∴∠AGH=180°﹣45°﹣75°=60°,
∵GH⊥AB,
∴∠GAH=30°,
∴AG=2GH,
∴BF=![]() AE=
AE=![]() (AG+EG),
(AG+EG),
∴BF=2![]() GH+
GH+![]() EG.
EG.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(a+2)x2+2ax+a﹣1的图象与x轴有交点,且关于x的分式方程![]() +1=
+1=![]() 的解为整数,则所有满足条件的整数a之和为( )
的解为整数,则所有满足条件的整数a之和为( )
A.﹣4B.﹣6C.﹣8D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,甲地到乙地的路程为450千米,一辆大货车从甲地前往乙地运送物资,行驶1小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过半小时修好大货年后以原速原路返甲地,小汽车在返程途中当走到一半路程时发现有重要物品落在大货车上,于是立即掉头以原速追赶大货车,追上大货车取下物品(取物品时间忽略不计)后以原速原路返回甲地,大货车修好后以原速前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则当小汽车第二次追上大货车时,大货车距离乙地_____千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,C为BD上一点,使得CA=CD,过点C作CE∥AD交AB于点E,过点D作DF⊥AD交AC的处长线于点F.
(1)若CD=3,求AF的长;
(2)若∠B=30°,∠ADC=40°,求证:AC=EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知点A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
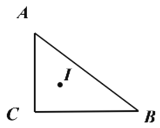
【题目】在Rt△ABC中,∠C=90°,AB=10,BC=8,AC=6.点I为△ABC三条角平分线的交点,则点I到边AB的距离为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com