
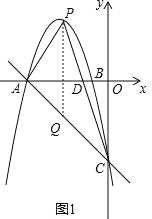
【题目】如图1,抛物线y=ax2﹣6x+c与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.
(1)求该抛物线所对应的函数解析式;
(2)若点P的坐标为(﹣2,3),请求出此时△APC的面积;
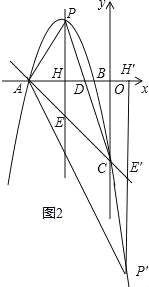
(3)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图2.
①若∠APE=∠CPE,求证:=;
②△APE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.

【答案】(1)y=﹣x2﹣6x﹣5;(2)15;(3)证明见解析;(4)能,P(﹣1,0)或(﹣2,3)或(,﹣7﹣6).
【解析】
试题分析:(1)把B、C坐标代入 解析式中可求得a,c的值,解析式即可求出;(2)过P作PQ⊥x轴交AC于点Q.由条件易求AC解析式.把P点横坐标到直线AC解析式中求出Q点坐标.则△CPQ与△APQ面积可求出,从而△APC面积可求;(3)①易证AP=PD,AH=DH,△PHD ∽△COD,设OH=p.则PH=-p2+6p-5,DH=AH=5-p,OD=2p-5,利用=,求出p值,求的AH,OH的长,再根据平行线分线段成比例,得出=,可证明结论;②设P(x,﹣x2﹣6x﹣5),则E(x,﹣x﹣5),分类讨论:当PA=PE,易得点P与B点重合,此时P点坐标为(﹣1,0);当AP=AE,如图2,利用PH=HE得到|﹣x2﹣6x﹣5|=|﹣x﹣5|,当E′A=E′P,如图2,AE′= E′H′= (x+5),P′E′=x2+5x,则x2+5x= (x+5),然后分别解方程求出x可得到对应P点坐标.
试题解析:(1)把B(-1,0)、C(0,-5)坐标代入y=ax2﹣6x+c中,得![]() ,解得
,解得![]() ,∴抛物线解析式为y=﹣x2﹣6x﹣5;(2)设直线AC的解析式为y=mx+n,把A(﹣5,0),C(0,﹣5)代入得
,∴抛物线解析式为y=﹣x2﹣6x﹣5;(2)设直线AC的解析式为y=mx+n,把A(﹣5,0),C(0,﹣5)代入得![]() ,解得
,解得![]() ,∴直线AC的解析式为y=﹣x﹣5,作PQ∥y轴交AC于Q,如图1,则Q(﹣2,﹣3),∴PQ=3﹣(﹣3)=6,∴S△APC=S△APQ+S△CPQ=PQ5=×6×5=15;(3)①∵∠APE=∠CPE,PH⊥AD,∴AP=PD,∴AH=DH.设OH=p,则PH=-p2+6p-5,DH=AH=5-p,OD=2p-5. ∵∠PHD=∠DOC=90°,∠PDH=∠ODC,∴△PHD ∽△COD,∴=,∴
,∴直线AC的解析式为y=﹣x﹣5,作PQ∥y轴交AC于Q,如图1,则Q(﹣2,﹣3),∴PQ=3﹣(﹣3)=6,∴S△APC=S△APQ+S△CPQ=PQ5=×6×5=15;(3)①∵∠APE=∠CPE,PH⊥AD,∴AP=PD,∴AH=DH.设OH=p,则PH=-p2+6p-5,DH=AH=5-p,OD=2p-5. ∵∠PHD=∠DOC=90°,∠PDH=∠ODC,∴△PHD ∽△COD,∴=,∴![]() ,解得p1=,p2=5(舍去).∴OH=,AH=.∵OC∥HE,∴==.②能.设P(x,﹣x2﹣6x﹣5),则E(x,﹣x﹣5),当PA=PE,因为∠PEA=45°,所以∠PAE=45°,则点P与B点重合,此时P点坐标为(﹣1,0);当AP=AE,如图2,则PH=HE,即|﹣x2﹣6x﹣ 5|=|﹣x﹣5|,解﹣x2﹣6x﹣5=﹣x﹣5得x1=﹣5(舍去),x2=0(舍去);解﹣x2﹣6x﹣5=x+5得x1=﹣5(舍去),x2=﹣2,此时P点坐标为(﹣2,3);当E′A=E′P,如图2,AE′= E′H′= (x+5),P′E′=﹣x﹣5﹣(﹣x2﹣6x﹣5)=x2+5x,则x2+5x= (x+5),解得x1=﹣5(舍去),x2=,此时P点坐标为(,﹣7﹣6),综上所述,满足条件的P点坐标为(﹣1,0),(﹣2,3),(,﹣7﹣6).
,解得p1=,p2=5(舍去).∴OH=,AH=.∵OC∥HE,∴==.②能.设P(x,﹣x2﹣6x﹣5),则E(x,﹣x﹣5),当PA=PE,因为∠PEA=45°,所以∠PAE=45°,则点P与B点重合,此时P点坐标为(﹣1,0);当AP=AE,如图2,则PH=HE,即|﹣x2﹣6x﹣ 5|=|﹣x﹣5|,解﹣x2﹣6x﹣5=﹣x﹣5得x1=﹣5(舍去),x2=0(舍去);解﹣x2﹣6x﹣5=x+5得x1=﹣5(舍去),x2=﹣2,此时P点坐标为(﹣2,3);当E′A=E′P,如图2,AE′= E′H′= (x+5),P′E′=﹣x﹣5﹣(﹣x2﹣6x﹣5)=x2+5x,则x2+5x= (x+5),解得x1=﹣5(舍去),x2=,此时P点坐标为(,﹣7﹣6),综上所述,满足条件的P点坐标为(﹣1,0),(﹣2,3),(,﹣7﹣6).


科目:初中数学 来源: 题型:
【题目】下列说法错误的是 ( )
A. 等腰三角形的高、中线、角平分线互相重合
B. 三角形两边的垂直平分线的交点到三个顶点距离相等
C. 等腰三角形的两个底角相等
D. 等腰三角形顶角的外角是底角的二倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A.x3﹣x=x(x2﹣1)B.x2+y2=(x+y)(x﹣y)
C.(a+4)(a﹣4)=a2﹣16D.m2+4m+4=(m+2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
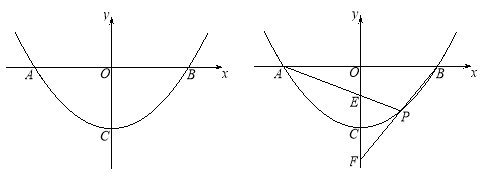
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
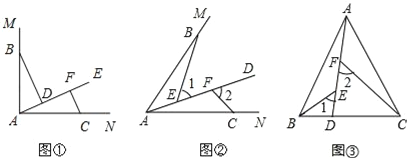
【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com