
如图,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知A点坐标为(a,0),B点坐标为(0,b),且a,b满足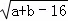 +|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
+|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
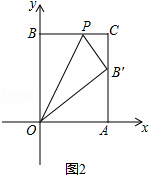
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
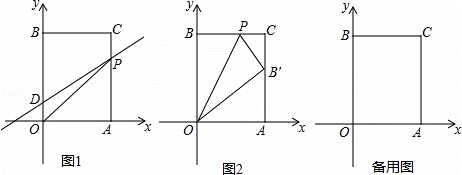
解:(1)∵a,b满足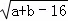 +|2a﹣b﹣2|=0,
+|2a﹣b﹣2|=0,
∴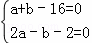 ,解得
,解得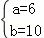 ,
,
∴点坐标为(6,0),B点坐标为(0,10),
∴C(6,10),
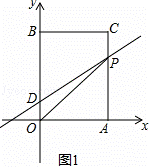
设此时直线DP解析式为y=kx+b,如图1,
将D(0,2),C(6,10)代入得: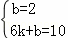 ,
,
解得: ,
,
则此时直线DP解析式为y=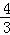 x+2;
x+2;
(2)①当点P在线段AC上时,OD=2,高为6,S=6;
当点P在线段BC上时,OD=2,高为6+10﹣t=16﹣t,S=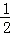 ×2×(16﹣t)=﹣t+16;
×2×(16﹣t)=﹣t+16;
②设P(m,10),则PB=PB′=m,如图2,
∵OB′=OB=10,OA=6,
∴AB′=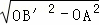 =8,
=8,
∴B′C=10﹣8=2,
∵PC=6﹣m,
∴m2=22+(6﹣m)2,解得m=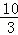
则此时点P的坐标是(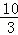 ,10);
,10);
(3)存在,理由为:
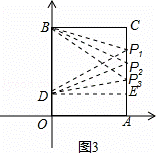
若△BDP为等腰三角形,分三种情况考虑:如图3,
①当BD=BP1=OB﹣OD=10﹣2=8,
在Rt△BCP1中,BP1=8,BC=6,
根据勾股定理得:CP1=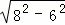 =2
=2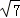 ,
,
∴AP1=10﹣2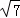 ,即P1(6,10﹣2
,即P1(6,10﹣2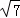 );
);
②当BP2=DP2时,此时P2(6,6);
③当DB=DP3=8时,
在Rt△DEP3中,DE=6,
根据勾股定理得:P3E=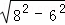 =2
=2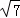 ,
,
∴AP3=AE+EP3=2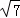 +2,即P3(6,2
+2,即P3(6,2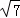 +2),
+2),
综上,满足题意的P坐标为(6,6)或(6,2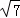 +2)或(6,10﹣2
+2)或(6,10﹣2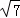 ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知a,b,c为△ABC的三边长,则关于x的一元二次方程4x2+4(a+b)x+c2=0的根的情况( )
A. 有两个不相等的实数根 B. 没有实数根
C. 有两个相等的实数根 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
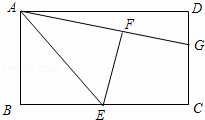
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c的图象如图所示,则下列结论①abc<0,②b2﹣4ac>0,③2a+b>0,④a+b+c<0,⑤ax2+bx+c+2=0的解为x=﹣0,其中正确的有( )个.
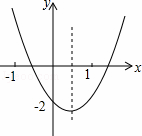
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
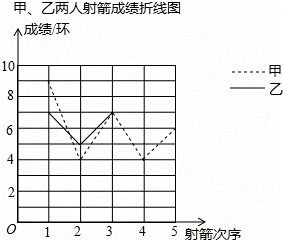
社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,他们的成绩被绘制成了如下的统计图表:
甲、乙两人射箭成绩统计表
第1次 第2次 第3次 第4次 第5次
甲成绩 9 4 7 a 6
乙成绩 7 5 7 b 5
请根据统计图表解答下列问题:
(1)a= 、b= ;
(2)请你在折线统计图中补全表示乙成绩变化情况的折线图;
(3)请你运用方差的知识,对甲、乙两人的成绩进行分析,说明谁将被选中参加集训.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com