
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B向点B运动,设运动时间为t秒(t>0)
(1)AC边上是否存在点P,使得PA=PB?若存在,求出t的值;若不存在,说明理由;
(2)若点P恰好在△ABC的角平分线上,请求出t的值,说明理由.

【答案】(1)t=![]() ;(2)t=2或
;(2)t=2或![]() 或
或![]() 或
或![]()
【解析】
(1)根据线段垂直平分线的性质得到PA=PB,从而分别表示出PC、BC、BP的长,利用勾股定理列出方程求解即可;
(2)当点P在顶点处时就是在角平分线上,然后再分点P在AC和∠ABC的角平分线的交点处和点P在BC和∠BAC的角平分线的交点处利用相似三角形列式求得t值即可.
解:(1)如图1,设存在点P,使得PA=PB,
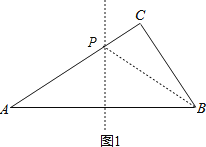
此时PA=PB=2t,PC=4-2t,
在Rt△PCB中,
PC2+CB2=PB2,
即:(4-2t)2+32=(2t)2,
解得:t=![]() ,
,
∴当t=![]() 时,PA=PB;
时,PA=PB;
(2)当点P在点C或点B处时,一定在△ABC的角平分线上,
∵∠ACB=90°,AB=5cm,BC=3cm,
∴AC=4cm,
当点P在点C处时,
∵t=4÷2=2s;
点P在点B处时,
∴t=(4+3)÷2=![]() ;
;
当点P在∠ABC的角平分线上时,作PM⊥AB于点M,如图2,
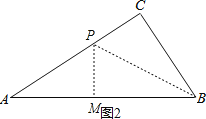
此时AP=2t,PC=PM=4-2t,
∵△APM∽△ABC,
∴AP:AB=PM:BC,
即:2t:5=(4-2t):3,
解得:t=![]() ;
;
当点P在∠CAB的平分线上时,作PN⊥AB,如图3,
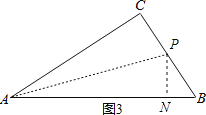
此时BP=7-2t,PN=PC=(2t-4),
∵△BPN∽△BAC,
∴BP:BA=PN:AC,
即:(7-2t):5=(2t-4):4,
解得:t=![]() ,
,
综上,当t=2s或![]() s或
s或![]() s或
s或![]() s时,点P在△ABC的角平分线上.
s时,点P在△ABC的角平分线上.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
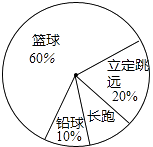
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为个;进球数的中位数为个,众数为个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD= 3,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,PE+PB的最小值 ______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30cm.
(结果精确到1cm.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,sin55°≈0.8,cos55°≈0.6,tan55°≈1.4)
(1)求B点到OP的距离;
(2)求滑动支架的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为圆上一点,AD和过点C的切线互相垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=6,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N.若BM+CN=7,则MN的长为( )

A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com