练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知如图，则下列叙述不正确的是（　　）

    A. 点O不在直线AC上

    B. 射线AB与射线BC是指同一条射线

    C. 图中共有5条线段

    D. 直线AB与直线CA是指同一条直线

    【答案】B

    【解析】

    根据点与直线的关系可知点O不在直线AC上，故A说法正确，不符合题意；

    射线表示方法是端点字母在前，故B错误，符合题意；

    图中有线段AB、AC、BC、OB、OC，共5条，故C说法正确，不符合题意；

    直线表示方法是用直线上两个点表示，没有先后顺序，故D正确，不符合题意．

    A、点O不在直线AC上，故A说法正确，不符合题意；

    B、射线AB与射线BC不是指同一条射线，故B错误，符合题意；

    C、图中有线段AB、AC、BC、OB、OC，共5条，故C说法正确，不符合题意；

    D、直线AB与直线CA是指同一条直线，故D正确，不符合题意．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们运用图（Ⅰ）中大正方形的面积可表示为（a+b）2，也可表示为c3+4（ab），即（a+b）2=c2+4（ab）由此推导出一个重要的结论a2+b2=c2，这个重要的结论就是著名的“勾股定理”．这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．

    （1）请你用图（Ⅱ）（2002年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形的较大的直角边长都为a，较小的直角边长都为b，斜边长都为c）．

    （2）请你用（Ⅲ）提供的图形进行组合，用组合图形的面积表达式验证：（x+2y）2=x2+4xy+4y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知AM∥CN，点B为平面内一点，AB⊥BC于B．

    （1）如图1，直接写出∠A和∠C之间的数量关系________；

    （2）如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；

    （3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场元旦期间举行优惠活动，对甲、乙两种商品实行打折出售，打折前，购买5间甲商品和1件乙商品需要84元，购买6件甲商品和3件乙商品需要108元，元旦优惠打折期间，购买50件甲商品和50件乙商品仅需960元，这比不打折前节省多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在¨ABCD中，过点D作DE⊥AB与点E，点F在边CD上，DF=BE,连接AF,BF

    （1）求证：四边形BFDE是矩形；

    （2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=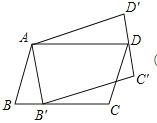

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE，若DE=BF，则下列结论：

    ①CF=AE；②OE=OF；③图中共有四对全等三角形；④四边形ABCD是平行四边形；其中正确结论的是_____________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地电话拨号上网有两种收费方式，用户可以任选其一：（A）计时制，0.05元∕分；（B）包月制，50元∕分（限一部个人住宅电话上网）；此外，每种上网方式都附加通信费0.02元∕分。

    （1）某用户某月上网时间为x分钟，则该用户在A、B两种收费方式下应支付费用各多少元？

    （2）如果一个月内上网200分钟和300分钟，按两种收费方式各需交费多少元？

    （3）是否存在某一时间，会出现两种收费方式一样的情况吗？求出这时的上网时间？

    （4）如果某人一个月上网20小时，那么应选用哪一种方式较为合算？如果小明的妈妈准备办理这种业务，你能告诉她如何选择更加合算吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A、B两个村庄的坐标分别为（2，2）、（7，4），一辆汽车从原点O出发，在x轴上行驶．

    （1）汽车行驶到什么位置时离村庄A最近？写出此位置的坐标．

    （2）汽车行驶到什么位置时离村庄B最近？写出此位置的坐标．

    （3）请在图中画出汽车到两村庄的距离和最短的位置，并求出此最短的距离和．

    查看答案和解析>>

    同步练习册答案