Question

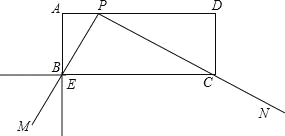
【题目】如图，在矩形ABCD中，AB=3，AD=10，将∠MPN的顶点P在矩形ABCD的边AD上滑动，在滑动过程中，始终保持∠MPN=90°，射线PN经过点C，射线PM交直线AB于点E，交直线BC于点F．

（1）求证：△AEP∽△DPC；

（2）在点P的运动过程中，点E与点B能重合吗？如果能重合，求DP的长；

（3）是否存在这样的点P使△DPC的面积等于△AEP面积的4倍？若存在，求出AP的长；若不存在，请证明理由．

Answer 1

【答案】(1)证明详见解析；(2)点E与点B能重合，B，E重合时DP的长为1或9；(3) 存在满足条件的点P，AP=1.5.

【解析】

试题分析：（1）根据矩形的性质，推出∠D=∠A=90°，再由直角三角形的性质，得出∠PCD+∠DPC=90°，又因∠CPE=90°，推出∠EPA+∠DPC=90°，∠PCD=∠EPA，从而证明△CDP∽△PAE；

（2）利用当B，E重合时，利用已知得出△ABP∽DPC，进而求出DP的长即可；

（3）假设存在满足条件的点P，设DP=x，则AP=10﹣x，由△CDP∽△PAE知，求出DP即可．

试题解析：（1）∵四边形ABCD是矩形，

∴∠D=∠A=90°，CD=AB=6，

∴∠PCD+∠DPC=90°，

又∵∠CPE=90°，

∴∠EPA+∠DPC=90°，

∴∠PCD=∠EPA，

∴△AEP∽△DPC；

（2）假设在点P的运动过程中，点E能与点B重合，

当B，E重合时，

∵∠BPC=90°，

∴∠APB+∠DPC=90°，

∵∠DPC+∠DCP=90°，

∴∠DCP=∠APB，

∵∠A=∠D，

∴△ABP∽DPC，

∴，

即，

解得：DP=1或9，

∴B，E重合时DP的长为1或9；

（3）存在满足条件的点P，

∵△CDP∽△PAE，

根据使△DPC的面积等于△AEP面积的4倍，得到两三角形的相似比为2，

∴=2，

即=2，

解得AP=1.5.