
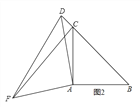
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACBĪŖČń½Ē£¬µćDĪŖBC±ßÉĻŅ»¶Æµć£¬Į¬½ÓAD£¬ŅŌADĪŖÖ±½Ē±ßĒŅŌŚADµÄÉĻ·½×÷µČŃüÖ±½ĒČż½ĒŠĪADF£®
£Ø1£©ČēĶ¼1£¬ČōAB=AC£¬”ĻBAC=90”ć£¬µ±µćDŌŚĻ߶ĪBCÉĻŹ±£Ø²»ÓėµćBÖŲŗĻ£©£¬
Ö¤Ć÷£ŗ”÷ACF”Õ”÷ABD
£Ø2£©ČēĶ¼2£¬µ±µćDŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻŹ±£¬ĘäĖüĢõ¼ž²»±ä£¬²ĀĻėCFÓėBDµÄŹżĮæ¹ŲĻµŗĶĪ»ÖĆ¹ŲĻµŹĒŹ²Ć“£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ČēĶ¼3£¬ČōAB”ŁAC£¬”ĻBAC”Ł90”ć£¬”ĻBCA=45”ć£¬µćDŌŚĻ߶ĪBCÉĻŌĖ¶Æ£Ø²»ÓėµćBÖŲŗĻ£©£¬ŹŌĢ½¾æCFÓėBDĪ»ÖĆ¹ŲĻµ£®



”¾“š°ø”æ¼ū½āĪö
”¾½āĪö”æ£Ø1£©øł¾ŻĶ¬½ĒµÄÓą½ĒĻąµČĒó³ö”ĻCAF=”ĻBAD£¬Č»ŗóĄūÓĆ”°±ß½Ē±ß”±Ö¤Ć÷”÷ACFŗĶ”÷ABDČ«µČ£¬
£Ø2£©ĻČĒó³ö”ĻCAF=”ĻBAD£¬Č»ŗóÓė¢ŁµÄĖ¼Ā·ĻąĶ¬Ēó½ā¼“æÉ£»
£Ø3£©¹żµćA×÷AE”ĶAC½»BCÓŚE£¬æɵƔ÷ACEŹĒµČÖ±½ĒČż½ĒŠĪ£¬øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹæɵĆAC=AE£¬”ĻAED=45”ć£¬ŌŁøł¾ŻĶ¬½ĒµÄÓą½ĒĻąµČĒó³ö”ĻCAF=”ĻEAD£¬Č»ŗóĄūÓĆ”°±ß½Ē±ß”±Ö¤Ć÷”÷ACFŗĶ¼ŪAEDČ«µČ£¬øł¾ŻČ«µČČż½ĒŠĪ¶ŌÓ¦½ĒĻąµČæɵƔĻACF=”ĻAED£¬Č»ŗóĒó³ö”ĻBCF=90”ć£¬“Ó¶ųµĆµ½CF”ĶBD.
½ā£ŗ£Ø1£©”ß”ĻBAC=90”ć£¬”÷ADFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻCAF+”ĻCAD=90”ć£¬”ĻBAD+”ĻACD=90”ć£¬AD=AF
”ą”ĻCAF=”ĻBAD£¬””””””
ŌŚ”÷ACFŗĶ”÷ABDÖŠ£¬
AB=AC£¬”ĻCAF=”Ļ£¬AD=AF£¬
”ą”÷ACF”Õ”÷ABD£ØSAS£©
£Ø2£©CF”ĶBD£¬
ČēĶ¼2£¬”ß”÷ADFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąAD=AF£¬
”ß”ĻCAB=”ĻDAF=90”ć£¬
”ą”ĻCAB+”ĻCAD=”ĻDAF+”ĻCAD£¬
¼“”ĻCAF=”ĻBAD£¬””
ŌŚ”÷ACFŗĶ”÷ABDÖŠ£¬
AB=AC£¬”ĻCAF=”ĻBAD£¬AD=AF£¬
”ą”÷ACF”Õ”÷ABD£ØSAS£©£¬””
”ąCF=BD£¬”ĻACF=”ĻB£¬
”ßAB=AC£¬”ĻBAC=90”ć£¬”ą”ĻB=”ĻACB=45”ć£¬
”ą”ĻBCF=”ĻACF+”ĻACB=45”ć+45”ć=90”ć£¬
”ąCF”ĶBD””
£Ø3£©CF”ĶBD
ČēĶ¼3£¬¹żµćA×÷AE”ĶAC½»BCÓŚE£¬
”ß”ĻBCA=45”ć£¬
”ą”÷ACEŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąAC=AE£¬”ĻAED=45”ć£¬
”ß”ĻCAF+”ĻCAD=90”ć£¬”ĻEAD+”ĻCAD=90”ć£¬
”ą”ĻCAF=”ĻEAD£¬””””
ŌŚ”÷ACFŗĶ”÷AEDÖŠ£¬
AC=AE£¬”ĻCAF=”ĻEAD£¬AD=AF£¬””
”ą”÷ACF”Õ”÷AED£ØSAS£©£¬””””
”ą”ĻACF=”ĻAED=45”ć£¬
”ą”ĻBCF=”ĻACF+”ĻBCA=45”ć+45”ć=90”ć£¬
”ąCF”ĶBD£®””””””
”°µć¾¦”±“ĖĢāŹĒČż½ĒŠĪ×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖČ«µČČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬µČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ£¬øł¾ŻĶ¬½ĒµÄÓą½ĒĻąµČĒó³öĮ½±ßµÄ¼Š½ĒĻąµČŹĒÖ¤Ć÷Čż½ĒŠĪČ«µČµÄ¹Ų¼ü£¬“ĖĄąĢāÄæµÄĢŲµćŹĒø÷Š”ĢāĒó½āĖ¼Ā·Ņ»°ć¶¼ĻąĶ¬.


 æŖŠÄĮ·Ļ°æĪæĪĮ·Óėµ„ŌŖ¼ģ²āĻµĮŠ“š°ø
æŖŠÄĮ·Ļ°æĪæĪĮ·Óėµ„ŌŖ¼ģ²āĻµĮŠ“š°ø æŖŠÄŹŌ¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
æŖŠÄŹŌ¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ŃĻĀĮŠø÷Ź½·Ö½āŅņŹ½
£Ø1£©3ax2+6axy+3ay2
£Ø2£©a2£Øx©y£©©b2£Øx©y£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
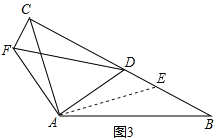
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻACB=2”ĻB£¬ČēĶ¼¢Ł£¬µ±”ĻC=90”ć£¬ADĪŖ”ĻBACµÄ½ĒĘ½·ÖĻߏ±£¬ŌŚABÉĻ½ŲČ”AE=AC£¬Į¬½ÓDE£¬Ņ×Ö¤AB=AC+CD£®


£Ø1£©ČēĶ¼¢Ś£¬µ±”ĻC”Ł90”ć£¬ADĪŖ”ĻBACµÄ½ĒĘ½·ÖĻߏ±£¬Ļ߶ĪAB”¢AC”¢CDÓÖÓŠŌõŃłµÄŹżĮæ¹ŲĻµ?ĒėŠ“³öÄćµÄ²ĀĻė²¢Ö¤Ć÷£»
£Ø2£©ČēĶ¼¢Ū£¬µ±ADĪŖ”÷ABCµÄĶā½ĒĘ½·ÖĻߏ±£¬Ļ߶ĪAB”¢AC”¢CDÓÖÓŠŌõŃłµÄŹżĮæ¹ŲĻµ?ĒėŠ“³öÄćµÄ²ĀĻė£¬²¢¶ŌÄćµÄ²ĀĻėøųÓčÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
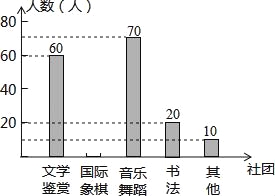
”¾ĢāÄæ”æ(2016ŗžÄĻŹ”ŌĄŃōŹŠµŚ21Ģā)Ä³Ń§Š£»·±£Ö¾ŌøÕߊ»į¶ŌøĆŹŠ³ĒĒųµÄæÕĘųÖŹĮæ½ųŠŠµ÷²é£¬“ÓČ«Äź365ĢģÖŠĖ껜³éČ”ĮĖ80ĢģµÄæÕĘųÖŹĮæÖøŹż£ØAQI£©Źż¾Ż£¬»ęÖĘ³öČż·ł²»ĶźÕūµÄĶ³¼ĘĶ¼±ķ£®Ēėøł¾ŻĶ¼±ķÖŠĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
AQIÖøŹż | ÖŹĮæµČ¼¶ | ĢģŹż£ØĢģ£© |
0©50 | ÓÅ | m |
51©100 | Į¼ | 44 |
101©150 | Ēį¶ČĪŪČ¾ | n |
151©200 | ÖŠ¶ČĪŪČ¾ | 4 |
201©300 | ÖŲ¶ČĪŪČ¾ | 2 |
300ŅŌÉĻ | ŃĻÖŲĪŪČ¾ | 2 |
£Ø1£©Ķ³¼Ę±ķÖŠm= £¬n= £®ÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬æÕĘųÖŹĮæµČ¼¶ĪŖ”°Į¼”±µÄĢģŹżÕ¼ %£»
£Ø2£©²¹Č«ĢõŠĪĶ³¼ĘĶ¼£¬²¢Ķعż¼ĘĖć¹Ą¼ĘøĆŹŠ³ĒĒųČ«ÄźæÕĘųÖŹĮæµČ¼¶ĪŖ”°ÓÅ”±ŗĶ”°Į¼”±µÄĢģŹż¹²¶ąÉŁĢģ£æ
£Ø3£©¾Żµ÷²é£¬ŃĻÖŲĪŪČ¾µÄ2Ģģ·¢ÉśŌŚ“ŗ½ŚĘŚ¼ä£¬Č¼·ÅŃĢ»Ø±¬Öń³ÉĪŖæÕĘųĪŪČ¾µÄŅ»øöÖŲŅŖŌŅņ£¬¾Ż“Ė£¬ĒėÄćĢį³öŅ»ĢõŗĻĄķ»Æ½ØŅ飮
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(2016¹ćĪ÷Ź”ŗŲÖŻŹŠµŚ21Ģā)ĪŖĮĖÉī»ÆæĪ³ĢøÄøļ£¬Ä³Š£»ż¼«æŖÕ¹Š£±¾æĪ³Ģ½ØÉč£¬¼Ę»®³ÉĮ¢”°ĪÄѧ¼ųÉĶ”±”¢”°¹ś¼ŹĻóĘå”±”¢”°ŅōĄÖĪčµø”±ŗĶ”°Źé·Ø”±µČ¶ąøöÉēĶÅ£¬ŅŖĒóĆæĪ»Ń§Éś¶¼×ŌÖ÷Ń”ŌńĘäÖŠŅ»øöÉēĶÅ£¬ĪŖ“Ė£¬Ė껜µ÷²éĮĖ±¾Š£²æ·ÖѧɜєŌńÉēĶŵÄŅāĻņ£®²¢½«µ÷²é½į¹ū»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼±ķ£Ø²»ĶźÕū£©£ŗ
Ń”ŌńŅāĻņ | ĪÄѧ¼ųÉĶ | ¹ś¼ŹĻóĘå | ŅōĄÖĪčµø | Źé·Ø | ĘäĖū |
ĖłÕ¼°Ł·Ö±Č | a | 20% | b | 10% | 5% |
øł¾ŻĶ³¼ĘĶ¼±ķµÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ē󱾓Ī³éŃłµ÷²éµÄѧɜ×ÜČĖŹż¼°a”¢bµÄÖµ£»
£Ø2£©½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ČōøĆŠ£¹²ÓŠ1300Ćūѧɜ£¬ŹŌ¹Ą¼ĘČ«Š£Ń”Ōń”°ŅōĄÖĪčµø”±ÉēĶŵÄѧɜČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
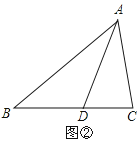
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻA=36”ć£¬ABµÄ“¹Ö±Ę½·ÖĻßDE½»ACÓŚD£¬½»ABÓŚE£¬ĻĀŹö½įĀŪ“ķĪóµÄŹĒ£Ø””””£©

A. BDĘ½·Ö”ĻABC B. ”÷BCDµÄÖܳ¤µČÓŚAB+BC
C. AD=BD=BC D. µćDŹĒĻ߶ĪACµÄÖŠµć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµćA£Øa©1£¬©4£©ÓėµćB£Ø©3£¬1©b£©¹ŲÓŚŌµć¶Ō³Ę£¬Ōņa+bµÄÖµĪŖ
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com