
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F. 
(1)若AC=6,AB=10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.
【答案】
(1)解:连接OD.设⊙O的半径为r.
∵BC切⊙O于点D,
∴OD⊥BC.
∵∠C=90°,
∴OD∥AC,
∴△OBD∽△ABC.
∴ ![]() =
= ![]() ,即10r=6(10﹣r).
,即10r=6(10﹣r).
解得r= ![]() ,
,
∴⊙O的半径为 ![]()
(2)解:四边形OFDE是菱形.理由如下:
∵四边形BDEF是平行四边形,
∴∠DEF=∠B.
∵∠DEF= ![]() ∠DOB,
∠DOB,
∴∠B= ![]() ∠DOB.
∠DOB.
∵∠ODB=90°,
∴∠DOB+∠B=90°,
∴∠DOB=60°.
∵DE∥AB,
∴∠ODE=60°.
∵OD=OE.
∴OD=DE.
∵OD=OF,
∴DE=OF.
又∵DE∥OF,
∴四边形OFDE是平行四边形.
∵OE=OF,
∴平行四边形OFDE是菱形.

【解析】(1)连接OD,设⊙O的半径为r,可证出△BOD∽△BAC,则 ![]() =
= ![]() ,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B=
,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B= ![]() ∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.
∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】从今年起,我市生物和地理会考实施改革,考试结果以等级形式呈现,分A、B、C、D四个等级.某校八年级为了迎接会考,进行了一次模拟考试,随机抽取部分学生的生物成绩进行统计,绘制成如下两幅不完整的统计图.
(1)这次抽样调查共抽取了名学生的生物成绩.扇形统计图中,D等级所对应的扇形圆心角度数为°;
(2)将条形统计图补充完整;
(3)如果该校八年级共有600名学生,请估计这次模拟考试有多少名学生的生物成绩等级为D?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、排球、其它等四个方面调查了若干名学生,并绘制成“折线统计图”与“扇形统计图”.请你根据图中提供的部分信息解答下列问题: 

(1)在这次调查活动中,一共调查了名学生;
(2)“足球”所在扇形的圆心角是度;
(3)补全折线统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°. 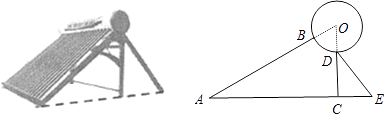
(1)求垂直支架CD的长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果保留三个有效数字,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为 ![]() 的正方形ABCD沿对角线AC平移,使点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是( )
的正方形ABCD沿对角线AC平移,使点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是( ) 
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC= ![]() .
. 
(1)求⊙O的半径;
(2)求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图. 
请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生共有人,在扇形图中,表示“其他球类”的扇形的圆心角为度;
(2)将条形图补充完整;
(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com