
【题目】如图,![]() ,点
,点![]() 是线段
是线段![]() 的一个三等分点,以点
的一个三等分点,以点![]() 为圆心,
为圆心,![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
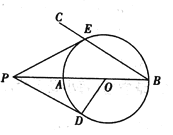
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 上的一动点,连接
上的一动点,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.
【答案】(1)见解析;(2)①60°,②120°.
【解析】
(1)连接![]() ,由
,由![]() ,得到
,得到![]() 为等边三角形,得到
为等边三角形,得到![]() ,即可得到
,即可得到![]() ,则结论成立;
,则结论成立;
(2)①连接BD,由圆周角定理,得到∠ABD=30°,则∠DBE=60°,又有∠BEP=120°,根据同旁内角互补得到PE//DB,然后证明![]() ,即可得到答案;
,即可得到答案;
②由圆周角定理,得∠ABD=60°,得到∠EBD=90°,然后由直径所对的圆周角为90°,得到![]() ,即可得到答案.
,即可得到答案.
证明:连接![]() ,
,
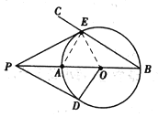
![]() ,
,
![]() .
.
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() .
.
![]() 点
点![]() 是
是![]() 的三等分点,
的三等分点,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 是
是![]() 的切线.
的切线.
(2)①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
如图,连接BD,
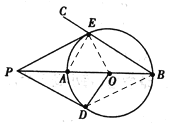
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB为直径,则∠AEB=90°,
由(1)知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴PE//DB,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;
故答案为:60°.
②当![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.
如图,连接AE、AD、DB,
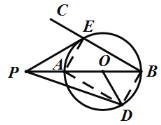
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB是直径,
∴![]() ,
,
∴四边形![]() 是矩形.
是矩形.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,则抽到数字“2”的概率是___________;
(2)从四张卡片中随机抽取2张卡片,请用列表或画树状图的方法求抽到“数字和为5”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示,请回答:
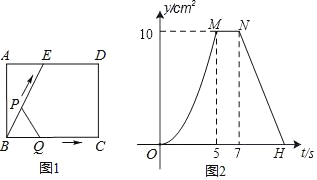
(1)线段BC的长为 cm.
(2)当运动时间t=2.5秒时,P、Q之间的距离是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
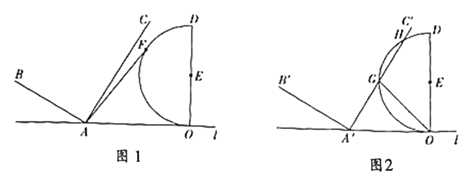
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为________;
的最大值为________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,AB=6,点P是射线BC上的一动点,过点P作PE⊥PA交直线CD于E,连AE.

(1)如图1,若BP=2,求DE的长;
(2)如图2,若AP平分∠BAE,连PD,求tan∠DPE的值;
(3)直线PD,AE交于点F,若BC=4PC,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB、CD是圆O的两条弦,交点为P.连接AD、BC. OM⊥ AD,ON⊥BC,垂足分别为M、N.连接PM、PN.
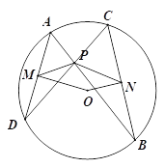
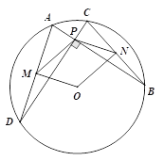
图1 图2
(1)求证:△ADP ∽△CBP;
(2)当AB⊥CD时,探究![]() PMO与
PMO与![]() PNO的数量关系,并说明理由;
PNO的数量关系,并说明理由;
(3)当AB⊥CD时,如图2,AD=8,BC=6, ∠MON=120°,求四边形PMON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为数学实验“先行示范校”,一数学活动小组带上高度为1.5m的测角仪BC,对建筑物AO进行测量高度的综合实践活动,如图,在BC处测得直立于地面的AO顶点A的仰角为30°,然后前进40m至DE处,测得顶点A的仰角为75°.
(1)求∠CAE的度数;
(2)求AE的长(结果保留根号);
(3)求建筑物AO的高度(精确到个位,参考数据:![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
:![]() 沿
沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() .
.
(1)求抛物线![]() 的顶点坐标;
的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
① 当![]() 时,求抛物线
时,求抛物线![]() 和
和![]() 围成的封闭区域内(包括边界)整点的个数;
围成的封闭区域内(包括边界)整点的个数;
② 如果抛物线C1和C2围成的封闭区域内(包括边界)恰有![]() 个整点,求m取值范围.
个整点,求m取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,将两个全等的等腰直角三角形![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,若
,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合).
重合).
(1)求证:![]() ;
;
(2)在旋转过程中,试判断等式![]() 是否始终成立,若成立,请证明;若不成立,请说明理由.
是否始终成立,若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com