
【题目】在平面直角坐标系中,点![]()
![]() ,
,![]()
![]() ,将直线
,将直线![]() 平移与双曲线
平移与双曲线![]() 在第一象限的图象交于
在第一象限的图象交于![]() 、
、![]() 两点.
两点.
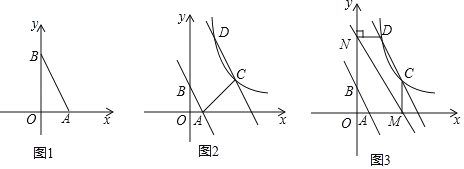
(1)如图1,将![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得
得![]() 与
与![]() 对应,
对应,![]() 与
与![]() 对应),在图1中画出旋转后的图形并直接写出
对应),在图1中画出旋转后的图形并直接写出![]() 、
、![]() 坐标;
坐标;
(2)若![]() ,
,
①如图2,当![]() 时,求
时,求![]() 的值;
的值;
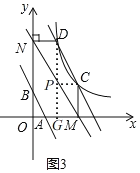
②如图3,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 有唯一公共点时,
有唯一公共点时,![]() 的值为 .
的值为 .
【答案】(1)作图见解析,![]() ,
,![]() ;(2)①k=6;②
;(2)①k=6;②![]() .
.
【解析】
(1)根据题意,画出对应的图形,根据旋转的性质可得![]() ,
,![]() ,从而求出点E、F的坐标;
,从而求出点E、F的坐标;
(2)过点![]() 作
作![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,根据相似三角形的判定证出
,根据相似三角形的判定证出![]() ,列出比例式,设
,列出比例式,设![]() ,根据反比例函数解析式可得
,根据反比例函数解析式可得![]() (Ⅰ);
(Ⅰ);
①根据等角对等边可得![]() ,可列方程
,可列方程![]() (Ⅱ),然后联立方程即可求出点D的坐标,从而求出k的值;
(Ⅱ),然后联立方程即可求出点D的坐标,从而求出k的值;
②用m、n表示出点M、N的坐标即可求出直线MN的解析式,利于点D和点C的坐标即可求出反比例函数的解析式,联立两个解析式,令△=0即可求出m的值,从而求出k的值.
解:(1)![]() 点
点![]()
![]() ,
,![]()
![]() ,
,
![]() ,
,![]() ,
,
如图1,

由旋转知,![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴负半轴上,
轴负半轴上,
![]() ,
,![]() ;
;
(2)过点![]() 作
作![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,

![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 在双曲线
在双曲线![]() 上,
上,
![]() ,
,
![]() (Ⅰ)
(Ⅰ)
①![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (Ⅱ),
(Ⅱ),
联立(Ⅰ)(Ⅱ)解得:![]() ,
,![]() ,
,
![]() ;
;
②如图3,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() (Ⅲ),
(Ⅲ),
![]() 双曲线
双曲线![]() (Ⅳ),
(Ⅳ),
联立(Ⅲ)(Ⅳ)得:![]() ,
,
即:![]() ,
,
![]() △
△![]() ,
,
![]() 直线
直线![]() 与双曲线
与双曲线![]() 有唯一公共点,
有唯一公共点,
![]() △
△![]() ,
,
![]() △
△![]() ,
,
![]() (舍
(舍![]() 或
或![]() ,
,
![]() ,
,
![]() .
.
故答案为:![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
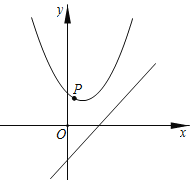
【题目】已知,抛物线y=![]() x2﹣x+2与直线y=x﹣2的图象如图,点P是抛物线上的一个动点,则点P到直线y=x﹣2的最短距离为( )
x2﹣x+2与直线y=x﹣2的图象如图,点P是抛物线上的一个动点,则点P到直线y=x﹣2的最短距离为( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
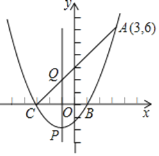
【题目】如图,一元二次方程x2+2x﹣3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)写出不等式ax2+bx+c≥0的解集;
(3)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标;
(4)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
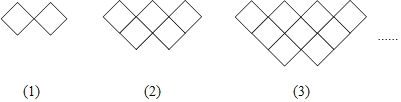
【题目】如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(n)个图形中面积为1的正方形的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件成本40元,出于营销考虑,要求每件售价不得低于40元,但物价部门要求每件售价不得高于60元.据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每涨1元,每天就少售出2件,设单价上涨![]() 元
元![]() .
.
(1)求当![]() 为多少时每天的利润是1350元?
为多少时每天的利润是1350元?
(2)设每天的销售利润为![]() ,求销售单价为多少元时,每天利润最大?最大利润是多少?
,求销售单价为多少元时,每天利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
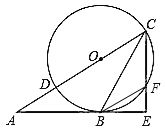
【题目】如图,已知Rt△ACE中,∠AEC=90°,CB平分∠ACE交AE于点B,AC边上一点O,⊙O经过点B、C,与AC交于点D,与CE交于点F,连结BF。
(1)求证:AE是⊙O的切线;
(2)若![]() ,AE=8,求⊙O的半径;
,AE=8,求⊙O的半径;
(3)在(2)条件下,求BF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
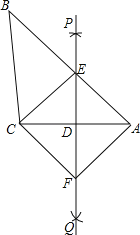
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若ED=6,AE=10,则菱形AECF的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
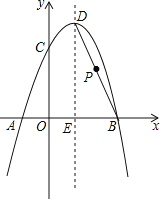
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com