
| A�� | �٢ڢۢ� | B�� | �٢ۢ� | C�� | �٢ڢ� | D�� | �٢ڢ� |
���� ͨ�������¶���ɶԢٽ����жϣ��������¶����ԭ����ת��Ϊx2+x-2=0����������ʽ�ֽⷨ�ⷽ�̣���ɶԢڽ����жϣ��������¶����ԭ����ʽ��ת��Ϊ$\left\{\begin{array}{l}{4-2x-6��0}\\{1+x-5��0}\end{array}\right.$��Ȼ��ͨ���ⲻ��ʽ��ɶԢ۽����жϣ��������¶����ԭ������ϵʽת��Ϊy=x2-x-2��Ȼ����ݶ��κ���ͼ���ϵ�����������Ԣܽ����жϣ�
��� �⣺1?3=12+1��3-=2�����Ԣ���ȷ��
����x?1=0��Ϊx2+x-2=0�����x1=-2��x2=1�����Ԣ���ȷ��
����ʽ��$\left\{\begin{array}{l}{��-2��?x-4��0}\\{1?x-3��0}\end{array}\right.$��Ϊ$\left\{\begin{array}{l}{4-2x-6��0}\\{1+x-5��0}\end{array}\right.$�����-1��x��4�����Ԣ���ȷ��
����y=x?��-1����Ϊy=x2-x-2����x=1ʱ��y=x2-x-21-1-2=-2�����Ե㣨1��-2���ں���y=x?��-1����ͼ���ϣ����Ԣ���ȷ��
��ѡA��
���� ���⿼���������붨�����ж�һ���������䣬�������⣮�������ⶼ��������ͽ�����������ɣ���������֪�������������֪�����Ƴ������һ���������д�ɡ��������ô������ʽ�� ��Щ�������ȷ����������֤ʵ�ģ����������������������


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
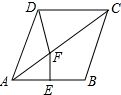 ��ͼ������ABCD�У���BAD=76�㣬AB�Ĵ�ֱƽ����EF��AC��F�����CDF�Ķ���Ϊ��������
��ͼ������ABCD�У���BAD=76�㣬AB�Ĵ�ֱƽ����EF��AC��F�����CDF�Ķ���Ϊ��������| A�� | 66�� | B�� | 52�� | C�� | 104�� | D�� | 86�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABCD�����ԲO��ˮƽ���������ڵ�A����֪ԲO�İ뾶Ϊ4����$\widehat{BC}$=2$\widehat{AB}$������û�л���������£���ԲO���ҹ�����ʹ��O�������ƶ���66�У����ʱ��������еĻ�Ϊ��������
��ͼ������ABCD�����ԲO��ˮƽ���������ڵ�A����֪ԲO�İ뾶Ϊ4����$\widehat{BC}$=2$\widehat{AB}$������û�л���������£���ԲO���ҹ�����ʹ��O�������ƶ���66�У����ʱ��������еĻ�Ϊ��������| A�� | $\widehat{AB}$ | B�� | $\widehat{BC}$ | C�� | $\widehat{CD}$ | D�� | $\widehat{DA}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
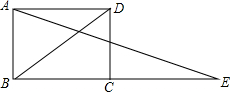 ��ͼ���ھ���ABCD�У�AB=2��AD=2$\sqrt{3}$����E��BC���ӳ����ϣ���BD=CE������AE�����E�Ķ���Ϊ��������
��ͼ���ھ���ABCD�У�AB=2��AD=2$\sqrt{3}$����E��BC���ӳ����ϣ���BD=CE������AE�����E�Ķ���Ϊ��������| A�� | 15�� | B�� | 20�� | C�� | 30�� | D�� | 45�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
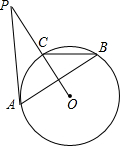 ��ͼ��PA���O�����ڵ�A��PO����O�ڵ�C����B���Ż�CBA��һ�㣬����P=26�㣬���ABC�Ķ���Ϊ��������
��ͼ��PA���O�����ڵ�A��PO����O�ڵ�C����B���Ż�CBA��һ�㣬����P=26�㣬���ABC�Ķ���Ϊ��������| A�� | 26�� | B�� | 64�� | C�� | 32�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com