练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．若关于x的方程2x-3k=5（x-k）-14的解为x=2，则k=-4．

    分析 把x=2代入方程计算即可求出k的值．

    解答 解：把x=2代入方程得：4-3k=5（2-k）-14，
    去括号得：4-3k=10-5k-14，
    移项合并得：2k=-8，
    解得：k=-4，
    故答案为：-4．

    点评 此题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．若二次函数y=ax2-2x-1的图象和x轴有交点，则a的取值范围为（　　）
    A．a＞-1B．a＞-1且a≠0C．a≥-1D．a≥-1且a≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：（$\sqrt{12}×\sqrt{8}+12\sqrt{\frac{1}{6}}-\sqrt{54}$）$÷2\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，ABCD是正方形，F是CD的中点，E是BC边上的一点，下列条件中，不能推出△ABE与△ECF相似的是（　　）
    A．∠AEB=∠FECB．∠AEF=90°C．E是BC的中点D．$BE=\frac{2}{3}BC$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．（1）分解因式：9a2（x-y）+4b2（y-x）
    （2）化简：$\frac{{a}^{2}-{b}^{2}}{a-b}$÷（2+$\frac{{a}^{2}+{b}^{2}}{ab}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在RT△ABC中，∠C=90°，CA=CB，D是AB边上一点，E是AC边上一动点，（不与A、C重合），DE⊥DF，DF交射线BC于F点，设AE=x．
    （1）若AC=BC=6，AD：DB=1：2，以CE为直径的⊙O与直线DE相切，同时也直线DF相切，求x的值．
    （2）若AC=BC=6，AD：DB=1：2，以CE为直径的⊙O，是否存在实数x，使⊙O与直线AB相切？若存在，求出x的值；若不存在，请说明理由．
    （3）若AC=BC=6，AD：DB=1：1，以EF为直径作⊙M，若EF=$2\sqrt{5}$，求$\frac{CE}{CF}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在平面直角坐标系中xOy，二次函数y=ax2-2ax+3的图象与x轴分别交于点A、B，与y轴交于点C，AB=4，动点P从B点出发，沿x轴负方向以每秒1个单位长度的速度移动．过P点作PQ垂直于直线BC，垂足为Q．设P点移动的时间为t秒（t＞0），△BPQ与△ABC重叠部分的面积为S．
    （1）求这个二次函数的关系式；
    （2）求S与t的函数关系式；
    （3）将△BPQ绕点P逆时针旋转90°，当旋转后的△BPQ与二次函数的图象有公共点时，求t的取值范围（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，把一个木制正方体的表面涂上颜色，然后将正方体的棱分成相等的四份，并做上标记，得到许多小正方体．问
    （1）有64个小正方体；
    （2）有24个小正方体只有两面涂有颜色
    （3）有8个小正方体只有3面都涂了颜色．
    （4）有8个小正方体6面都未涂色．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

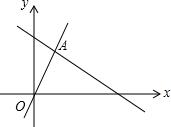    6．如图，函数y=2x和y=ax+2b的图象相交于点A（m，2），则不等式2x≤ax+2b的解集为（　　）
    A．x＜1B．x＞1C．x≥1D．x≤1

    查看答案和解析>>

    同步练习册答案