
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
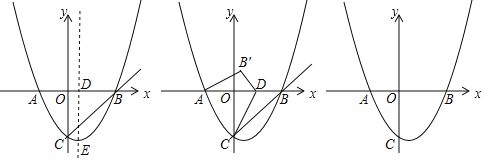
(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
【答案】(1)![]() ,A(﹣2,0);(2)E到BC的最大距离为
,A(﹣2,0);(2)E到BC的最大距离为![]() ;(3)①D1(0,0);D2(3
;(3)①D1(0,0);D2(3![]() ,0);②B′坐标为(0,3
,0);②B′坐标为(0,3![]() )或(-3
)或(-3![]() )或(
)或(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)求出B,C两点的坐标,代入抛物线解析式即可得出答案;
(2)设E点横坐标为m,则F(m,m3),过点E作EH⊥BC于点H,EF=yFyE=![]() ,利用二次函数的性质可求出E到直线BC的距离的最大值;
,利用二次函数的性质可求出E到直线BC的距离的最大值;
(3)①点B′在以C为圆心,CB为半径的圆C上.所以满足条件的B′有两个,分别位于y轴、x轴,结合对称的性质解答即可;
②分不同的情况进行讨论:
(Ⅰ)当点B′位于y轴上,易得点B′的坐标;
(Ⅱ)如图3,连接CB′,构造菱形DB′CB,根据菱形的性质求得B′(3![]() ,3);
,3);
(Ⅲ)∠B′AD=45°,如图4,连接CB′,过点B′分别作坐标轴的垂线,垂足为E、F,在直角△CFB′中,由勾股定理知m2+(5m)2=(3![]() )2,解出m即可;
)2,解出m即可;
(Ⅳ)如图5,∠AB′D=45°,连接CB’,过点B′作y轴的垂线,垂足为点F,由轴对称性质可得当∠AB′D=45°时,点A在线段CB′上,结合勾股定理求得m的值,进而求得符合条件的点B′的坐标.
(1)∵B点与C点是直线y=x﹣3与x轴、y轴的交点.
∴B(3,0),C(0,﹣3),
∴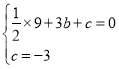 ,解得:
,解得: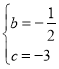 ,
,
∴抛物线的解析式为![]() ,
,
令y=0,则![]() ,
,
解得x1=﹣2,x2=3,
∴A(﹣2,0);(2)设E点到直线BC的距离为d,E点横坐标为m,F(m,m﹣3),
∵B(3,0),C(0,﹣3),
∴∠OBC=45°,
如图1,过点E作EH⊥BC于点H,
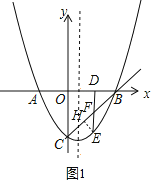
则△EFH为等腰直角三角形,
∴EH=![]() ,
,
EF=yF﹣yE=m﹣3﹣(![]() ),
),
=![]() (0≤m≤3),
(0≤m≤3),
=![]() ,
,
当![]() 时,EF的最大值为
时,EF的最大值为![]() ,
,
∴d=![]() EF=
EF=![]() =
=![]() .
.
即E到BC的最大距离为![]() ;
;
(3)①点B′在以C为圆心,CB为半径的圆C上;
(Ⅰ)当B′点落在x轴上时,D1(0,0);
(Ⅱ)当B′点落在y轴上时,如图2,CB′=CB=3![]() ,
,
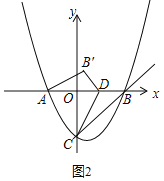
∵∠OB′D=45°
∴OD=OB’=3![]() ﹣3,
﹣3,
∴![]() ;
;
②分别画出图形进行讨论求解:
(Ⅰ)∠B′DA=45°时,如图2,OB′=3![]() ﹣3,B′(0,3
﹣3,B′(0,3![]() ﹣3)
﹣3)
(Ⅱ)如图3,连接CB′,∠B′DA=∠CBD=45°,

∴DB′∥BC,可得四边形DB′CB是菱形,
B′(﹣3![]() ,﹣3).
,﹣3).
(Ⅲ)∠B′AD=45°,如图4,连接CB′,过点B′分别作坐标轴的垂线,垂足为E、F,
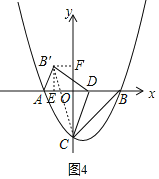
设线段FB’的长为m,B′E=AE=2﹣m,可得CF=5﹣m,
在直角三角形CFB’中,m2+(5﹣m)2=(3![]() )2,
)2,
解得m=![]() ,
,
故B′(![]() ),
),
(Ⅳ)如图5,∠AB′D=45°,连接CB’,过点B′作y轴的垂线,垂足为点F,
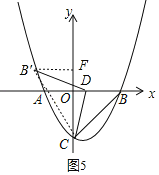
由轴对称性质可得,∠CB′D=∠CBD=45°,所以当∠AB′D=45°时,点A在线段CB′上,
∴![]() ,
,
设线段FB′的长为2m,FC=3m,(2m)2+(3m)2=![]() ,
,
解得:m=![]() ,B′
,B′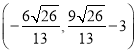 ,
,
综合以上可得B′坐标为(0,![]() )或
)或![]() 或(
或(![]() )或
)或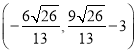 .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形 ABCD 中,过点 A 作 AE⊥DC 交 DC 的延长线于点 E,过点 D 作DF // EA 交 BA 的延长线于点 F.
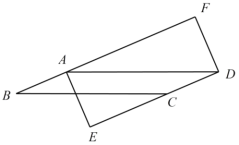
(1)求证:四边形 AEDF 是矩形;
(2)连接BD,若 AB=AE=2,tan FAD ![]() ,求 BD 的长.
,求 BD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )

A.30°B.35°C.40°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为0或4时,函数值都为-3,当自变量
的值为0或4时,函数值都为-3,当自变量![]() 的值为-1或5时,函数值为2.
的值为-1或5时,函数值为2.
探究过程如下,请补充完整.
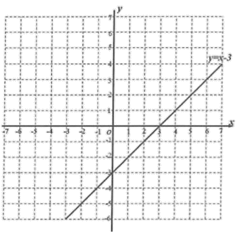
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有4个解,则k的取值范围为 ;
有4个解,则k的取值范围为 ;
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 和点
和点![]() 在抛物线
在抛物线![]() 上.
上.
(Ⅰ)求该抛物线的解析式和顶点坐标,并求出![]() 的值;
的值;
(Ⅱ)求点![]() 关于
关于![]() 轴对称点
轴对称点![]() 的坐标,并在
的坐标,并在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最短,求此时点
最短,求此时点![]() 的坐标;
的坐标;
(Ⅲ)平移抛物线![]() ,记平移后点
,记平移后点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为
的对应点为![]() ,点
,点![]() 是
是![]() 轴上的定点.
轴上的定点.
①当抛物线向左平移到某个位置时,![]() 最短,求此时抛物线的解析式;
最短,求此时抛物线的解析式;
②![]() 是
是![]() 轴上的定点,当抛物线向左平移到某个位置时,四边形
轴上的定点,当抛物线向左平移到某个位置时,四边形![]() 的周长最短,求此时抛物线的解析式(直接写出结果即可)
的周长最短,求此时抛物线的解析式(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
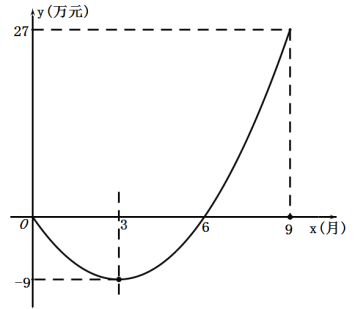
【题目】大学生小李和同学一起自主创业开办了一家公司,公司对经营的盈亏情况在每月的最后一天结算一次.在1-12月份中,该公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系.
(1)求y与x函数关系式.
(2)该公司从哪个月开始“扭亏为盈”(当月盈利)? 直接写出9月份一个月内所获得的利润.
(3)在前12 个月中,哪个月该公司所获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费,如图是张磊家2018年2月和3月所交电费的收据.
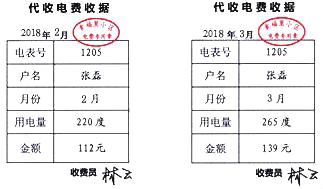
(1)该市规定的第一阶梯电价和第二阶梯电价单价分别为多少?
(2)张磊家4月份家庭支出计划中电费为160元,他家最大用电量为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
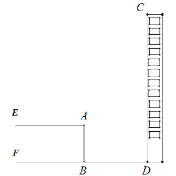
【题目】为了测量学校附近新盖大楼的高度,数学实践活动小组,借助大楼旁边高30米的空中操场进行测量.其中![]() 米,
米,![]() 地面
地面![]() ,小华站在操场的
,小华站在操场的![]() 处观测大楼顶点
处观测大楼顶点![]() 的仰角为
的仰角为![]() 、大楼底端
、大楼底端![]() 的俯角为
的俯角为![]() ,请根据题中的信息求出大楼
,请根据题中的信息求出大楼![]() 的高度.
的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com