Question

7．设△ABC的面积为1，如图①，将边BC、AC分别2等分，BE₁、AD₁相交于点O，△AOB的面积记为S₁；如图②，将边BC、AC分别3等分，BE₁、AD₁相交于点O，△AOB的面积记为S₂；以此类推，△AOB的面积记为S₃、S₄、S₅、…．则：
（1）S₁=$\frac{1}{3}$；
（2）S_n=$\frac{1}{2n+1}$．（用含n的代数式表示，其中n为正整数）

Answer 1

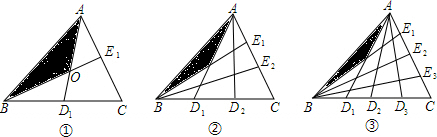
分析 连接D₁ E₁ 可得：△OD₁ E₁∽△OAB，又相似三角形的性质可知∴$\frac{O{D}_{1}}{OA}=\frac{{D}_{1}{E}_{1}}{AB}$=$\frac{1}{2}$，故S_△OAB=$\frac{2}{3}$S${\;}_{△AB{D}_{1}}$，而S${\;}_{△AB{D}_{1}}$=$\frac{1}{2}$S_△ABC=$\frac{1}{2}$，所以S₁=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$，同法可
得出S_n=$\frac{1}{2n+1}$．

解答 解：（1）如下图所示：连接D₁ E₁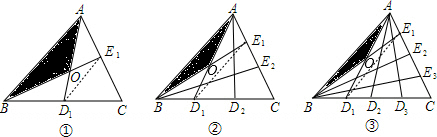 


在图①中：
∵点D₁、E₁ 分别是边BC、AC的中点，
∴AB∥$\frac{1}{2}$D₁ E₁，
∴△OD₁ E₁∽△OAB，
∴$\frac{O{D}_{1}}{OA}=\frac{{D}_{1}{E}_{1}}{AB}$=$\frac{1}{2}$
∴S_△OAB=$\frac{2}{3}$S${\;}_{△AB{D}_{1}}$，而S${\;}_{△AB{D}_{1}}$=$\frac{1}{2}$S_△ABC=$\frac{1}{2}$
∴S₁=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$
即：（1）的答案是$\frac{1}{3}$
（2）在△ABO与△D₁ E₁ O中，$\left\{\begin{array}{l}{\frac{C{E}_{1}}{CA}=\frac{C{D}_{1}}{CB}}\\{∠C=∠C}\end{array}\right.$
∴△OD₁ E₁∽△OAB（两边对应成比例，且夹角相等的两个三角形相似）
∴$\frac{O{D}_{1}}{OA}=\frac{{D}_{1}{E}_{1}}{AB}$=$\frac{2}{3}$，
∴S_△OAB=$\frac{3}{5}$S${\;}_{△AB{D}_{1}}$ 
∴S${\;}_{△AB{D}_{1}}$=$\frac{1}{3}$S_△ABC
∴S₂=$\frac{3}{5}$×$\frac{1}{3}$=$\frac{1}{5}$；
同理：S₃=$\frac{4}{7}$×$\frac{1}{4}$=$\frac{1}{7}$；
…
以此类推，S_n=$\frac{1}{2n+1}$
故：（2）的答案为$\frac{1}{2n+1}$

点评 本题考查了相似三角形的判定与性质、三角形的面积等知识点，解题的关键是利用相似三角形的性质获得线段OD₁ 与OA的比