
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左则,
点在原点的左则,![]() 点的坐标为
点的坐标为![]() ,与
,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
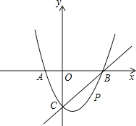
![]() 求这个二次函数的表达式;
求这个二次函数的表达式;
![]() 求出四边形
求出四边形![]() 的面积最大时的
的面积最大时的![]() 点坐标和四边形
点坐标和四边形![]() 的最大面积;
的最大面积;
![]() 连结
连结![]() 、
、![]() ,在同一平面内把
,在同一平面内把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() ,是否存在点
,是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 在直线
在直线![]() 找一点
找一点![]() ,使得
,使得![]() 为等腰三角形,请直接写出
为等腰三角形,请直接写出![]() 点坐标.
点坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,四边形
时,四边形![]() 的面积取最大值,最大值为
的面积取最大值,最大值为![]() ;(3)存在点
;(3)存在点![]() ,使四边形
,使四边形![]() 为菱形;(4)
为菱形;(4)![]() 点坐标为
点坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)直接代入B、C两点坐标即可求解解析式;
(2)过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,设
,设![]() ,求解直线BC解析式为
,求解直线BC解析式为![]() ,则可得
,则可得![]() ,观察图形,利用
,观察图形,利用![]() 即可求解;
即可求解;
(3)取![]() 的中点
的中点![]() ,过
,过![]() 作
作![]() 的垂线交抛物线于
的垂线交抛物线于![]() ,在
,在![]() 的延长线上取
的延长线上取![]() ,连接
,连接![]() 、
、![]() ,所得四边形
,所得四边形![]() 即为菱形;
即为菱形;
(4)设点![]() 的坐标为
的坐标为![]() ,则利用已知点C和O,写出用m表示的OC、PC、PO的表达式,再分别按
,则利用已知点C和O,写出用m表示的OC、PC、PO的表达式,再分别按![]() 、
、![]() 和
和![]() 三种情况进行讨论,分别求解m的值即可.
三种情况进行讨论,分别求解m的值即可.
解:![]() 将点
将点![]() 、
、![]() 代入
代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() ,
,
∴该二次函数的表达式为![]() .
.
![]() ∵点
∵点![]() ,点
,点![]() ,
,
∴直线![]() .
.

过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,如图
,如图![]() 所示.
所示.
设![]() ,则点
,则点![]() ,
,
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
∴点![]() .
.
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
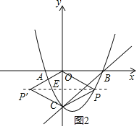
∵![]() ,
,![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 的面积取最大值,最大值为
的面积取最大值,最大值为![]() .
.
![]() 取
取![]() 的中点
的中点![]() ,过
,过![]() 作
作![]() 的垂线交抛物线于
的垂线交抛物线于![]() ,在
,在![]() 的延长线上取
的延长线上取![]() ,连接
,连接![]() 、
、![]() ,如图
,如图![]() 所示.
所示.
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 为菱形.
为菱形.
当![]() ,则有
,则有![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴存在点![]() ,使四边形
,使四边形![]() 为菱形.
为菱形.
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
![]() 为等腰三角形分三种情况:
为等腰三角形分三种情况:
①当![]() 时,
时,![]() ,
,
解得:![]() ,
,
此时点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
②当![]() 时,
时,![]() ,
,
解得:![]() 或
或![]() (舍去),
(舍去),
此时点![]() 的坐标为
的坐标为![]() ;
;
③当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.
综上可知:![]() 点坐标为
点坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标.
(1)点P的横坐标比纵坐标大1;
(2)点P在过点A(3,-2),且与x轴平行的直线上;
(3)点P到y轴的距离是到x轴距离的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AC=8,△ABC的面积为20,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,点E在△ABC外一点,CE⊥AE于点E,CE=![]() BC.
BC.
(1)作出△ABC的角平分线AD.(要求:尺规作图,不写作法,保留作图痕迹.)
(2)求证:∠ACE=∠B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口有一灯塔![]() ,灯塔
,灯塔![]() 的正东有
的正东有![]() 、
、![]() 两灯塔,以
两灯塔,以![]() 为直径的半圆区域内有若干暗礁,
为直径的半圆区域内有若干暗礁,![]() 海里,一船在
海里,一船在![]() 处测得灯塔
处测得灯塔![]() 、
、![]() 分别在船的
分别在船的
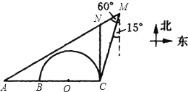
南偏西![]() 和南偏西
和南偏西![]() 方向,船沿
方向,船沿![]() 方向行驶
方向行驶![]() 海里恰好处在灯塔
海里恰好处在灯塔![]() 的正北方向
的正北方向![]() 处.
处.
![]() 求
求![]() 的长(精确到
的长(精确到![]() 海里);
海里);
![]() 若船继续沿
若船继续沿![]() 方向朝
方向朝![]() 行驶,是否有触礁的危险?
行驶,是否有触礁的危险?
(参考数值:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于某地供水管爆裂.该地供水部门组织工人进行抢修.供水部门距离抢修工地15千米.抢修车装载着所需材料先从供水部门出发,15分钟后,工人乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
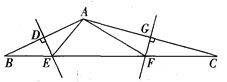
【题目】如图,△ABC中,AB、AC的垂直平分线分别交BC于点E、F.若△AEF的周长为12cm,则BC的长为____________________cm.若∠EAF=110°,则∠BAC=_____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com