
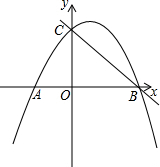
 在平面直角坐标系中,点O为坐标原点,直线y=-$\frac{2}{3}$x+6与x轴交于点B,过点B的抛物线y=ax2+bx-27a与直线y=-$\frac{2}{3}$x+6交于y轴上的C点.
在平面直角坐标系中,点O为坐标原点,直线y=-$\frac{2}{3}$x+6与x轴交于点B,过点B的抛物线y=ax2+bx-27a与直线y=-$\frac{2}{3}$x+6交于y轴上的C点.分析 (1)根据条件可求出点B和点C的坐标,然后运用待定系数法就可求出a、b的值;
(2)延长PQ交x轴于点G,如图1,设点P的横坐标为t,可求得PQ=$-\frac{2}{9}{t^2}+2t$.易证△BGQ∽△BOC,从而可求得BQ=$\frac{\sqrt{13}}{3}$(9-t),然后根据条件PQ=$\frac{\sqrt{13}}{3}$QB得到关于t的方程,解这个方程,就可解决问题;
(3)过点F作FH⊥MN于H,如图2.在(2)的条件下,可求出S△QOB,从而可求出MN的值.易证△DFN∽△COB,设DF=2m,根据相似三角形的性质及勾股定理可求出FN、DN、MF、FH、MH、DH、MD的值,从而得到MD=DN=4.设点M的横坐标为n,可得到MD=-$\frac{2}{9}$n2+2n=4,然后解这个方程,就可得到点M的坐标,根据MN=8就可得到点N的坐标.
解答 解:(1)∵直线$y=-\frac{2}{3}x+6$与x轴交于点B,与y轴交于点C,
∴令y=0,得$-\frac{2}{3}x+6=0$,解得x=9,则B(9,0);
令x=0,得y=$-\frac{2}{3}×0+6=6$,则C(0,6).
∵抛物线y=ax2+bx-27a过点B(9,0)、C(0,6),
∴$\left\{\begin{array}{l}0={9^2}a+9b-27a\\ 6=-27a\end{array}\right.$,
解得$\begin{array}{l}\left\{\begin{array}{l}a=-\frac{2}{9}\\ b=\frac{4}{3}\end{array}\right.\end{array}$,
∴a、b的值分别为-$\frac{2}{9}$、$\frac{4}{3}$;
(2)延长PQ交x轴于点G,如图1.
设点P的横坐标为t,则点Q的横坐标也为t.
∵P点在抛物线$y=-\frac{2}{9}{x^2}+\frac{4}{3}x+6$上,点Q在直线$y=-\frac{2}{3}x+6$上,
∴yP=$-\frac{2}{9}{t^2}+\frac{4}{3}t+6$,yQ=$-\frac{2}{3}t+6$,
∴PQ=$-\frac{2}{9}{t^2}+\frac{4}{3}t+6$-($-\frac{2}{3}t+6$)=$-\frac{2}{9}{t^2}+2t$.
∵B(9,0),C(0,6),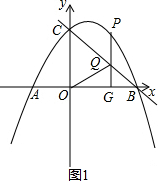 G(t,0),
G(t,0),
∴OB=9,OC=6,BG=9-t,
∴BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=3$\sqrt{13}$.
∵GQ∥OC,
∴△BGQ∽△BOC,
∴$\frac{BQ}{BC}$=$\frac{BG}{BO}$,
∴$\frac{BQ}{3\sqrt{13}}$=$\frac{9-t}{9}$,
∴BQ=$\frac{\sqrt{13}}{3}$(9-t).
∵PQ=$\frac{{\sqrt{13}}}{3}QB$,
∴$-\frac{2}{9}{t^2}+2t$=$\frac{{\sqrt{13}}}{3}•\frac{{\sqrt{13}}}{3}(9-t)$,
整理得2t2-31t+117=0,
解得:t1=9(舍去),${t_2}=\frac{13}{2}$,
∴PQ=$\frac{{\sqrt{13}}}{3}•\frac{{\sqrt{13}}}{3}(9-t)$=$\frac{13}{9}×\frac{5}{2}=\frac{65}{18}$;
(3)过点F作FH⊥MN于H,如图2.
由(2)得t=$\frac{13}{2}$,
∴yQ=$-\frac{2}{3}t+6$=$\frac{5}{3}$,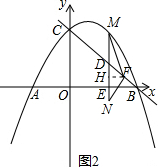
∴S△QOB=$\frac{1}{2}$×9×$\frac{5}{3}$=$\frac{15}{2}$,
∵$\frac{1}{4}$MN2-1=2S△QOB,
∴$\frac{1}{4}$MN2-1=15,
解得MN=8.
∵MN∥CD,∴∠NDB=∠OCB,
∵NF⊥BC,CO⊥AB,
∴∠DFN=∠COB=90°,
∴△DFN∽△COB,
∴$\frac{DF}{CO}$=$\frac{FN}{OB}$=$\frac{DN}{CB}$,
∴$\frac{DF}{6}$=$\frac{FN}{9}$=$\frac{DN}{3\sqrt{13}}$,
设DF=2m,则FN=3m,DN=$\sqrt{13}$m,MF=DF+FN=5m.
∴FH=$\frac{DF•FN}{DN}$=$\frac{2m•3m}{\sqrt{13}m}$=$\frac{6\sqrt{13}}{13}$m,
∴MH=$\sqrt{M{F}^{2}-F{H}^{2}}$=$\frac{17\sqrt{13}}{13}$m,
DH=$\sqrt{D{F}^{2}-F{H}^{2}}$=$\frac{4\sqrt{13}}{13}$m,
∴MD=MH-DH=$\sqrt{13}$m,
∴MD=DN.
∵MN=8,
∴MD=DN=4.
设点M的横坐标为n,则点D的横坐标也为n.
∵M点在抛物线$y=-\frac{2}{9}{x^2}+\frac{4}{3}x+6$上,点D在直线$y=-\frac{2}{3}x+6$上,
∴yM=-$\frac{2}{9}$n2+$\frac{4}{3}$n+6,yD=-$\frac{2}{3}$n+6,
∴MD=(-$\frac{2}{9}$n2+$\frac{4}{3}$n+6)-(-$\frac{2}{3}$n+6)=-$\frac{2}{9}$n2+2n=4,
解得n1=3(舍去),n2=6,
当n=6时,yM=-$\frac{2}{9}$×62+$\frac{4}{3}$×6+6=6.
∵MN=8,
∴yN=yM-8=6-8=-2,
∴N(6,-2).
点评 本题主要考查了抛物线及直线上点的坐标特征、用待定系数法求抛物线的解析式、相似三角形的判定与性质、勾股定理、解一元二次方程等知识,对运算能力的要求比较高,有一定的难度;将PQ及QB用t的代数式表示则是解决第(2)小题的关键,证到MD=DN则是解决第(3)小题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+2)2-1 | B. | y=2x2-1 | C. | y=2(x+2)2+1 | D. | y=2(x-1)2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
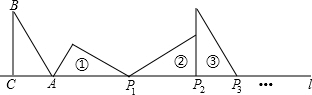
| A. | 2012+671$\sqrt{3}$ | B. | 2013+671$\sqrt{3}$ | C. | 2014+671$\sqrt{3}$ | D. | 2015+671$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | -$\frac{8}{7}$ | C. | $\frac{5}{3}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com