
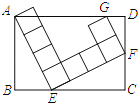
【题目】如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为( )
A.12![]() B.10
B.10![]() C.8
C.8![]() D.8+4
D.8+4![]()
【答案】C
【解析】
可设BE=x,CE=y,由题意可得△ABE≌ECF,并且△ECF∽△FDG,从而得出关于x、y的两个方程,求解后即可得出矩形ABCD的周长;
解:∵小正方形的面积为1,
∴小正方形的边长也为1,
设BE=x,CE=y,
∵∠AEB+∠CEF=90°,而∠EFC+∠CEF=90°,
∴∠AEB=∠EFC,
又∵∠B=∠C=90°,AE=EF=4,
∴△ABE≌ECF(AAS),
∴AB=EC=y,BE=CF=x,
∴由勾股定理可得x2+y2=42,
而同理可得∠EFC=∠FGD,且∠C=∠D=90°,
∴△ECF∽△FDG,
∴![]() ,
,
∴FD=![]() EC=
EC=![]() y,
y,
∵AB=CD,
∴y=x+![]() y,
y,
∴y=2x,将其代入x2+y2=42中
于是可得x=![]() ,y=
,y=![]() ,
,
而矩形ABCD的周长=2(x+y)+2y=5y=5×![]() =
= ![]() ;
;
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线 y x![]() bx c 的顶点为 P,与 x 轴交于 A,B 两点.若 A,B 两点间的距离为 m, n 是 m 的 函数,且表示 n 与 m 的函数关系的图象大致如图2所示,则 n 可能为( )
bx c 的顶点为 P,与 x 轴交于 A,B 两点.若 A,B 两点间的距离为 m, n 是 m 的 函数,且表示 n 与 m 的函数关系的图象大致如图2所示,则 n 可能为( )

A.PA ABB.PA ABC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)和一次函数y=mx+n的图象过格点(网格线的交点)B、P.
(x>0)和一次函数y=mx+n的图象过格点(网格线的交点)B、P.
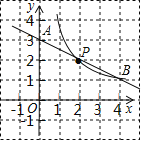
(1)求反比例函数和一次函数的解析式;
(2)观察图象,直接写出一次函数值大于反比例函数值时x的取值范围是: .
(3)在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点O,点P;
②矩形的面积等于k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
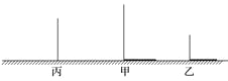
(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(2m+1)x+m﹣4的图象与x轴有两个公共点,m取满足条件的最小的整数
(1)求此二次函数的解析式
(2)当n≤x≤1时,函数值y的取值范围是﹣5≤y≤1﹣n,求n的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点分别为A(﹣2,1),B(﹣1,3),C(﹣2,4).
(1)画出△ABC关于原点O对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点O顺时针方向旋转90°得到的△A2B2C2,并写出点A2的坐标.
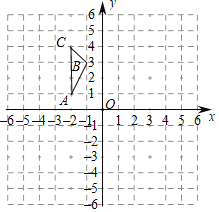
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com