
分析 (1)设该汽车租赁公司2月份A,B两种型号的汽油的使用量各是x升,y升,根据“A种型号的汽油均价为5.7元/升,B种型号的汽油价均价为6元/升,这个月共支付这两种型号汽油的费用为40800元,A、B两种型号的汽油均价都上调了0.6元/升,多支付这两种型号汽油的费用4200元.”列出方程组解答即可;
(2)根据(1)的数据表示出4月份的使用量和价格,算出总费用列出方程解答即可.
解答 解:(1)设该汽车租赁公司2月份A,B两种型号的汽油的使用量各是x升,y升,由题意得
$\left\{\begin{array}{l}{5.7x+6y=40800}\\{0.6x+0.6y=4200}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=4000}\\{y=3000}\end{array}\right.$
答:该汽车租赁公司2月份A,B两种型号的汽油的使用量各是4000升,3000升.
(2)由题意得
4000(1-m%)×6.3×(1+$\frac{m}{10}$)=4000×6.3,
解得m1=90,m2=0(不合题意舍去).
故m的值是90.
点评 考查了二元一次方程组的应用,一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程(组),再求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
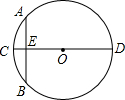 “圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?
“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com