
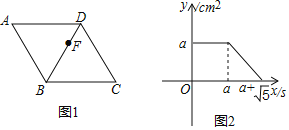
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为______.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
| … |
(1)可求得![]() ,第
,第![]() 个格子中的数为 ;
个格子中的数为 ;
(2)若前![]() 个格子中所填整数之和
个格子中所填整数之和![]() ,则
,则![]() 的值为多少?若
的值为多少?若![]() 的值为多少?
的值为多少?
(3)若![]() ,则
,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.
(1)求购买1个排球、1个篮球的费用分别是多少元?
(2)若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂家本周计划每天生产300辆摩托车,由于工厂实行轮休,每天上班人数不一定相等,实际每天生产与计划相比情况如下表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +7 | ﹣3 | +4 | +10 | ﹣9 | ﹣25 |
(1)本周六生产了多少辆摩托车?
(2)本周总产量与计划相比是增加了还是减少了?具体数量是多少?产量最多的一天比产量最少的一天多生产了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;

于是他立即原地调头追赶帽子,原地调转船头用了10分钟.
![]()
计算:
(1)求顺水速度,逆水速度是多少?
(2)从帽子丢失到发觉经过了多少时间?
(3)从发觉帽子丢失到捡回帽子经过了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
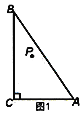
【题目】如图1.在△ABC中,∠ACB=90°,点P为△ABC内一点.
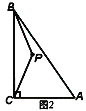
(1)连接PB、PC,将△BCP沿射线CA方向平移,得到△DAE,点B、C、P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,AB+BP=9,CE=![]() ,求AB的长.
,求AB的长.
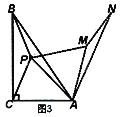
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=4,AB=8时,根据此图求PA+PB+PC的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com