
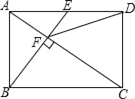
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() ;⑤S四边形CDEF=
;⑤S四边形CDEF=![]() S△ABF,其中正确的结论有( )
S△ABF,其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
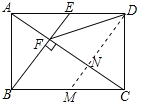
【解析】试题分析:过D作DM∥BE交AC于N,∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,AD=BC,∵BE⊥AC于点F,∴∠EAC=∠ACB,∠ABC=∠AFE=90°,∴△AEF∽△CAB,故①正确;
∵AD∥BC,∴△AEF∽△CBF,∴![]() ,∵AE=
,∵AE=![]() AD=
AD=![]() BC,∴
BC,∴![]() ,∴CF=2AF,故②正确,
,∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,∴四边形BMDE是平行四边形,∴BM=DE=![]() BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,故③正确;
BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,故③正确;
∵tan∠CAD=![]() ,而CD与AD的大小不知道,∴tan∠CAD的值无法判断,故④错误;
,而CD与AD的大小不知道,∴tan∠CAD的值无法判断,故④错误;
∵△AEF∽△CBF,∴![]() ,∴S△AEF=
,∴S△AEF=![]() S△ABF,S△ABF=
S△ABF,S△ABF=![]() S矩形ABCD,∵S△ABE=
S矩形ABCD,∵S△ABE=![]() S矩形ABCD,S△ACD=
S矩形ABCD,S△ACD=![]() S矩形ABCD,∴S△AEF=
S矩形ABCD,∴S△AEF=![]() S四边形ABCD,又∵S四边形CDEF=S△ACD﹣S△AEF=
S四边形ABCD,又∵S四边形CDEF=S△ACD﹣S△AEF=![]() S矩形ABCD﹣
S矩形ABCD﹣![]() S矩形ABCD=
S矩形ABCD=![]() S矩形ABCD,∴S四边形CDEF=
S矩形ABCD,∴S四边形CDEF=![]() S△ABF,故⑤正确;
S△ABF,故⑤正确;
故选B.


科目:初中数学 来源: 题型:
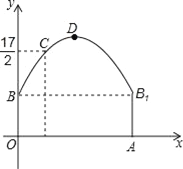
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点![]() 和
和![]() ,给出如下定义:如果
,给出如下定义:如果![]() ,那么称点Q为点P的“妫川伴侣”.
,那么称点Q为点P的“妫川伴侣”.
例如:点(5,6)的“妫川伴侣”为点(5,6),点(-5,6)的“妫川伴侣”为点(-5,-6).
(1)①点(2,1)的“妫川伴侣”为 ;②如果点A(3,-1),B(-1,3)的“妫川伴侣”中有一个在函数![]() 的图象上,那么这个点是 (填“点A”或“点B”).
的图象上,那么这个点是 (填“点A”或“点B”).
(2)①点![]() 的“妫川伴侣”点M的坐标为 ;②如果点
的“妫川伴侣”点M的坐标为 ;②如果点![]() 是一次函数y=x+2图象上点N的“妫川伴侣”,求点N的坐标.
是一次函数y=x+2图象上点N的“妫川伴侣”,求点N的坐标.
(3)如果点P(x,y)在函数![]() 的图象上,其“妫川伴侣”Q的纵坐标y'的取值范围是
的图象上,其“妫川伴侣”Q的纵坐标y'的取值范围是![]() ,那么实数a的取值范围是
,那么实数a的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(a)是正方形纸板制成的一副七巧板.
(1)请你在图(a)中给它的每一小块用①~⑦编号(编号直接标在每一小块对应图形内部的空白处;每小块只能与一个编号对应,每个编号只能和一个小块对应),并同时满足以下三个条件:
条件1:编号为①~③的三小块可以拼成一个轴对称图形;
条件2:编号为④~⑥的三小块可以拼成一个中心对称图形;
条件3:编号为⑦的小块是中心对称图形.
(2)请你在图(b)中画出编号为①~③的三小块拼出的轴对称图形;在图(c)中画出编号为④~⑥的三小块拼出的中心对称图形.(注意:没有编号不得分)

查看答案和解析>>
科目:初中数学 来源: 题型:
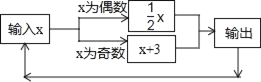
【题目】如图所示的运算程序中,若开始输入的x值为32,我们发现第一次输出的结果为16,第二次输出的结果为8,…,则第2019次输出的结果为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信,这五封信的重量分别是![]() .根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
业务种类 | 计费单位 | 资费标准/元 | 挂号费/(元/封) | 特制信封(元/个) |
挂号信 | 首重100g,每重20g | 0.8 | 3 | 0.5 |
续重101~2000g,每重100g | 2.00 | |||
特制信封 | 首重1000g内 | 5.00 | 3 | 1.0 |
(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?
(2)这五封信分别以怎样的方式寄出最合算?请说明理由.
(3)通过解答上述问题,你有何启示?(请你用一两句话说明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com