
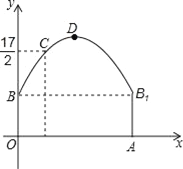
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
【答案】(1)拱顶D到地面OA的距离为10m;(2)这辆货车能安全通过;(3)两排灯的水平距离最小是4![]() m.
m.
【解析】试题分析:(1)先确定B点和C点坐标,然后利用待定系数法求出抛物线解析式,再利用配方法确定顶点D的坐标,从而得到点D到地面OA的距离;
(2)由于抛物线的对称轴为直线x=6,而隧道内设双向行车道,车宽为4m,则货运汽车最外侧与地面OA的交点为(2,0)或(10,0),然后计算自变量为2或10的函数值,再把函数值与6进行大小比较即可判断;
(3)抛物线开口向下,函数值越大,对称点之间的距离越小,于是计算函数值为8所对应的自变量的值即可得到两排灯的水平距离最小值.
解:(1)根据题意得B(0,4),C(3,![]() ),
),
把B(0,4),C(3,![]() )代入y=﹣
)代入y=﹣![]() x2+bx+c得
x2+bx+c得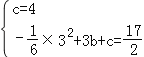 ,
,
解得![]() .
.
所以抛物线解析式为y=﹣![]() x2+2x+4,
x2+2x+4,
则y=﹣![]() (x﹣6)2+10,
(x﹣6)2+10,
所以D(6,10),
所以拱顶D到地面OA的距离为10m;
(2)由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y=![]() >6,
>6,
所以这辆货车能安全通过;
(3)令y=8,则﹣![]() (x﹣6)2+10=8,解得x1=6+2
(x﹣6)2+10=8,解得x1=6+2![]() ,x2=6﹣2
,x2=6﹣2![]() ,
,
则x1﹣x2=4![]() ,
,
所以两排灯的水平距离最小是4![]() m.
m.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
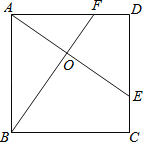
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其均分成四块小长方形,然后按图②的形状拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于__________.
(2)请用两种不同的方法求图②中阴影部分的面积.
方法1:__________ ;
方法2:__________ .
(3)观察图②,你能写出代数式:(m+n)2,(m-n)2,mn之间的等量关系吗?
_______________________ _ .
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,则(a-b)2=___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.
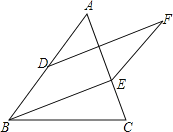
(1)猜想:DF与AE的关系是 ;
(2)试说明你猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
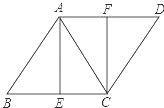
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.

(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是( )
A. 1米 B. 1.5米 C. 2米 D. 2.5米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com