练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．计算：（-$\frac{1}{3}$）2015×（-3）2016=（　　）
    A．$\frac{1}{3}$B．3C．-$\frac{1}{3}$D．-3

    分析 先将（-3）2016变形为（-3）2015×（-3），然后逆用积的乘方公式进行计算即可．

    解答 解：原式=（-$\frac{1}{3}$）2015×（-3）2015×（-3）
    =[（-$\frac{1}{3}$）×（-3）]2015×（-3）
    =1×（-3）
    =-3．
    故选：D．

    点评 本题主要考查的是积的乘方，逆用积的乘方公式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．当y=10时，代数式3y-1比4y-6的值小5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

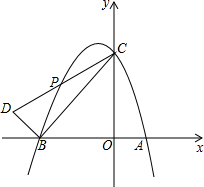    8．如图，抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A（2，0）、B两点，与y轴交于点C．
    （1）求b的值；
    （2）求抛物线的对称轴及顶点坐标；
    （3）以点B为直角顶点，BC为直角边作Rt△BCD，CD交抛物线于第二象限的点P，若PC=PD，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

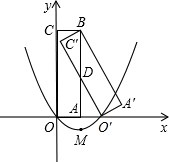    5．如图，矩形A′BC′O′是矩形OABC（边OA在x轴正半轴上，边OC在y轴正半轴上）绕B点逆时针旋转得到的，O′点在x轴的正半轴上，B点的坐标为（1，3）．
    （1）直接写出OA与O′A的数量关系；
    （2）如果二次函数y=ax2+bx+c（a≠0）的图象经过O、O′两点且图象顶点M的纵坐标为-1：
    ①在二次函数对称轴右侧的图象是否存在点P，使得△POM为直角三角形？若存在，请求出P点的坐标和四边形POMO′的面积；若不存在，请说明理由；
    ②若C′O′与AB相交于点D，在对称轴上是否存在一点Q，使得∠A′QD=∠BA′D？若存在，求出点Q坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

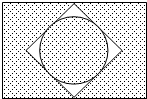    12．如图是“温州南”动车站前广场设计方案之一，其中大广场地面长方形的长200米，宽100米，大广场“含”一个边长为80米正方形广场，正方形广场又“含”一个半径为40米的圆形中心广场，按设计，图中阴影处铺设某种广场地砖．则广场地砖需要铺多少平方米？（π取3，结果精确到千位）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．体育课上，老师测量跳远成绩的依据是（　　）
    A．两点之间，线段最短
    B．垂线段最短
    C．过一点只有一条直线与已知直线垂直
    D．两点确定一条直线

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知如图①，在△ABC中，∠ABC、∠ACB的平分线交于点O，
    （1）若∠A=70°，则∠BOC=125°，试判断∠BOC与∠A存在的某种等量关系并证明；
    （2）如图②，在△ABC中，∠ABC、∠ACB的三等分线交于点O1、O2，则∠BO1C=$\frac{2}{3}×180°+\frac{1}{3}∠A，∠B{O_2}C=\frac{1}{3}×180°+\frac{2}{3}$∠A．
    根据以上信息解决下列问题：
    ①试找出它们的规律（n等分时，内部有n-1个点），n等分时∠BO1C=$\frac{n-1}{n}$×180°+$\frac{1}{n}$∠A，∠BOn-1C=$\frac{1}{n}×180°+\frac{n-1}{n}×∠A$．（用含n的式子表示），
    ②根据你的猜想，取n=4时，证明∠BO3C表达式仍然成立．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．设边长为a的正方形的面积为2．下列关于a的三种说法：①a是无理数；②a可以用数轴上的一个点来表示；
    ③1＜a＜2．其中，所有正确的序号是（　　）
    A．①②B．①③C．②③D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各式是由两个数的和或差的完全平方得到的展开式的是（　　）
    A．x2-x+$\frac{1}{4}$B．1+x2C．x2+xy+1D．x2+2x-1

    查看答案和解析>>

    同步练习册答案