
如图①,将两个完全相同的三角形纸片ABC与DEC重合放置,其中∠C=90°,∠B=∠E=30°。

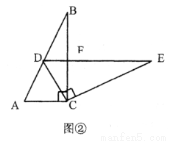
(1)如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,DE交BC于点F,则线段DF与AC有怎样的关系?请说明理由。
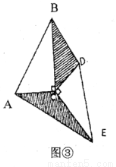
(2)当△DEC绕点C旋转到图③所示的位置时,设△BDC的面积为S1,△AEC的面积为S2。
猜想:S1与S2有怎样的数量关系?并证明你的猜想。
(1) DF∥AC;(2) S1=S2.
【解析】
试题分析:(1)根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
(2)过D点作DN⊥BC于N,AM⊥CE于M,先依据ASA求得△ACM≌△DCN求得AM=DN,然后根据等底等高的三角形面积相等.
试题解析:(1)DF∥AC;
【解析】
如图②所示,
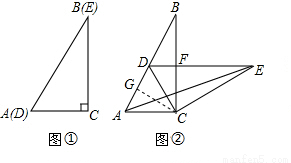
∵∠ACB=90°,∠B=∠E=30°,
∴∠A=∠CDE=60°,
∵AC=DC,
∴△ACD是等边三角形,
∴∠ACD=60°=∠CDE,
∴DF∥AC,
∴∠CFD=90°,∠DCF=30°,
∴DF=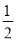 DC=
DC=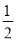 AC;
AC;
(2)猜想:S1=S2;
证明:过D点作DN⊥BC于N,AM⊥CE于M,

∵∠ECD=90°,
∴∠DCM=90°
∴∠DCN=90°-∠NCM,
又∵∠ACM=90°-∠NCM,
∴∠ACM=∠DCN,
在△ACM与△DCN中
∠ACM=∠DCN
AC=CD
∠AMC=∠DNC,
∴△ACM≌△DCN(ASA),
∴AM=DN,
又∵CE=BC,
∴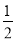 BC•DN=
BC•DN=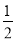 CE•AM,
CE•AM,
即S1=S2.
考点:全等三角形的判定与性质;等边三角形的判定与性质.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:2015届江西省高安市八年级下学期期末考试数学试卷(解析版) 题型:解答题
已知一次函数y=kx+b,当x=2时,y=﹣3,当x=1时,y=﹣1.
(1)求一次函数的解析式;
(2)若该一次函数的图形交x轴y轴分别于A、B两点,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源:2015届江西省八年级下学期第一次月考数学试卷(解析版) 题型:选择题
等腰三角形的一边为4,另一边为9,则这个三角形的周长为 ( )
A、17 B、22 C、13 D、17或22
查看答案和解析>>
科目:初中数学 来源:2015届江西省吉安市六校八年级下学期联考数学试卷(解析版) 题型:解答题
如图,△ABC中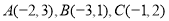
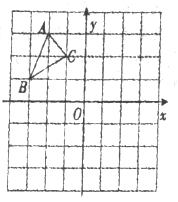
(1)画出△ABC关于x轴对称的△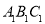
(2)将△ABC绕原点O旋转180°,画出旋转后的△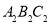 。
。
查看答案和解析>>
科目:初中数学 来源:2015届江苏省苏州市相城区八年级下学期期末考试数学试卷(解析版) 题型:选择题
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )
A.只有1个 B.可以有2个 C.可以有3个 D.有无数个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com