
【题目】如图1,在□ABCD中,![]() ,
,![]() ,
,![]() ,射线AE平分
,射线AE平分![]() 动点P以
动点P以![]() 的速度沿AD向终点D运动,过点P作
的速度沿AD向终点D运动,过点P作![]() 交AE于点Q,过点P作
交AE于点Q,过点P作![]() ,过点Q作
,过点Q作![]() ,交PM于点
,交PM于点![]() 设点P的运动时间为
设点P的运动时间为![]() ,四边形APMQ与四边形ABCD重叠部分面积为
,四边形APMQ与四边形ABCD重叠部分面积为![]()



![]() ______
______![]() 用含t的代数式表示
用含t的代数式表示![]()
![]() 当点M落在CD上时,求t的值.
当点M落在CD上时,求t的值.
![]() 求S与t之间的函数关系式.
求S与t之间的函数关系式.
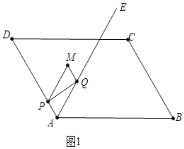
![]() 如图2,连结AM,交PQ于点G,连结AC、BD交于点H,直接写出t为何值时,GH与三角形ABD的一边平行或共线.
如图2,连结AM,交PQ于点G,连结AC、BD交于点H,直接写出t为何值时,GH与三角形ABD的一边平行或共线.
【答案】(1)![]() (2)
(2)![]() (3)
(3)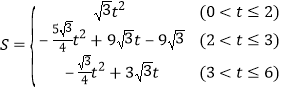
(4)![]() 或
或![]() 或4s时,GH与三角形ABD的一边平行或共线
或4s时,GH与三角形ABD的一边平行或共线
【解析】
(1)由题意得△APQ是直角三角形,∠PAQ=60°,利用正切值即可求得PQ的值;
(2)如图2,由题意可知∠D=60°,四边形APMQ为平行四边形,得∠DPQ=60°,所以△DPM是等边三角形,则DP=MP=AQ=2PA,即6-t=2t,解得t=2;
(3)如图1,3,4,分![]() ,
,![]() ,
,![]() 三种情况讨论,分别计算出三种情况下的重叠部分面积为
三种情况讨论,分别计算出三种情况下的重叠部分面积为![]() 与t的函数关系式即可;
与t的函数关系式即可;
(4)如图5,6,7,分别计算出当![]() ,或GH与BD重合,或
,或GH与BD重合,或![]() 时,三种情况下t的值即可.
时,三种情况下t的值即可.
![]() 如图1中,
如图1中,
![]() ,AE平分
,AE平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
故答案为![]()
![]() 如图2中,
如图2中,
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,四边形APMQ是平行四边形,
,四边形APMQ是平行四边形,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 当
当![]() 时,如图1中,重叠部分是平行四边形APMQ,
时,如图1中,重叠部分是平行四边形APMQ,![]() ;
;
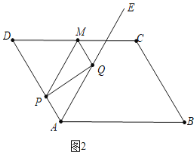
![]() 如图3中,当
如图3中,当![]() 时,重叠部分五边形APSTQ,
时,重叠部分五边形APSTQ,
易证△MST为等边三角形,则MT=MP﹣PS=MP﹣DP=2t﹣(6﹣t)=3t﹣6,
故![]() .
.
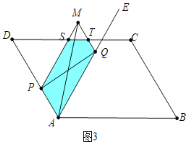
![]() 如图4中,当
如图4中,当![]() 时,重叠部分是四边形PSTA.
时,重叠部分是四边形PSTA.
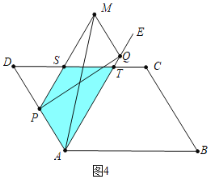
则![]()
综上所述,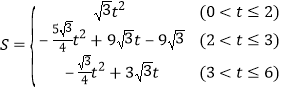 .
.
![]() 如图5中,当
如图5中,当![]() 时,
时,![]() ,
,
![]() 点M在线段CD上,此时
点M在线段CD上,此时![]() .
.
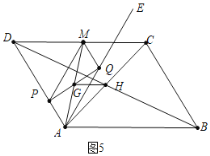
如图6中,当GH与BD重合时,作![]() 交DA的延长线于T.
交DA的延长线于T.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]()
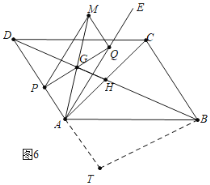
如图7中,当![]() 时,易证B,C,Q共线,
时,易证B,C,Q共线,

可得![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,
![]() ,
,
综上所述,![]() 或
或![]() 或4s时,GH与三角形ABD的一边平行或共线.
或4s时,GH与三角形ABD的一边平行或共线.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
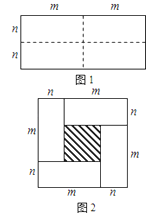
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2, (m﹣n)2, mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 分别是
分别是![]() 轴上位于原点两侧的两点,点
轴上位于原点两侧的两点,点![]() 在第一象限,直线
在第一象限,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求![]() ;
;
(2)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(3)若![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
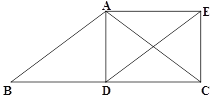
【题目】如图,在△ABC中,AB = AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
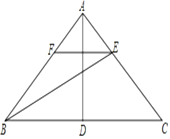
【题目】如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=40°,求∠BAD的度数;
(2)求证:FB=FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放置在水平桌面上的台灯的灯臂AB长为40 cm,灯罩BC长为30 cm,底座厚度为2 cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少厘米?(结果精确到0.1 cm,参考数据:![]() ≈1.732)
≈1.732)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点![]() 的直线
的直线![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
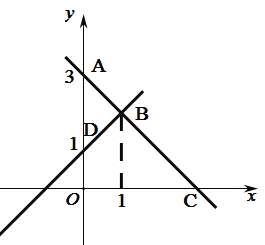
(1)求![]() 的坐标及直线
的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
(3)![]() 为
为![]() 的图象与
的图象与![]() 轴的交点,求四边形
轴的交点,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 过点
过点![]() 和
和![]() 对于该二次函数有如下说法:
对于该二次函数有如下说法:
①它的图象与![]() 轴有两个公共点;
轴有两个公共点;
②若存在一个正数![]() ,使得当
,使得当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而减小,则
的增大而减小,则![]() ;若存在一个负数
;若存在一个负数![]() ,使得当
,使得当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大,则
的增大而增大,则![]() ;
;
③若将它的图象向左平移![]() 个单位后过原点,则
个单位后过原点,则![]() ;
;
④若当![]() 时的函数值与
时的函数值与![]() 时的函数值相等,则当
时的函数值相等,则当![]() 时的函数值为
时的函数值为![]() .
.
其中正确的说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com