Question

10．△ABC中，∠A=90°，∠C=30°，AB=1，两个动点P和Q同时从点A出发，P沿AC运动，Q沿AB，BC运动，结果两个动点同时到达点C．
（1）点Q的速度是点P速度的几倍？
（2）当AP为何值时，△APQ的面积为$\frac{3\sqrt{3}}{16}$？

Answer 1

分析 （1）根据P、Q同时出发、同时到达，知P、Q时间一致，路程比即等于速度比可得；
（2）分点Q在AB、BC上运动讨论，点Q在AB上运动时面积最大值小于$\frac{3\sqrt{3}}{16}$情况排除，点Q在BC上运动时，求出AP边上的高，根据面积列出方程求解可得AP的值．

解答 解：（1）∵在△ABC中，∠A=90°，∠C=30°，AB=1，
∴BC=2，AC=$\sqrt{3}$，
∵两个动点P，Q同时从A点出发，点P沿AC运动，点Q沿AB，BC运动，两点同时到达点C
∴Q的速度是P的速度的（2+1）÷$\sqrt{3}$=$\sqrt{3}$倍；

（2）设AP=x，由（1）知Q点运动路程为$\sqrt{3}$x，
①点Q在AB上运动，0≤$\sqrt{3}x$≤1，即0≤x≤$\frac{\sqrt{3}}{3}$，
当点Q与点B重合时，△APQ的面积最大；
此时AQ=AB=1，则AP=$\frac{\sqrt{3}}{3}$，
故△APQ的面积为：$\frac{1}{2}×\frac{\sqrt{3}}{3}×1$=$\frac{\sqrt{3}}{6}$＜$\frac{3\sqrt{3}}{16}$；
②点Q在BC上运动，1＜$\sqrt{3}x$≤3，即$\frac{\sqrt{3}}{3}$＜x≤$\sqrt{3}$；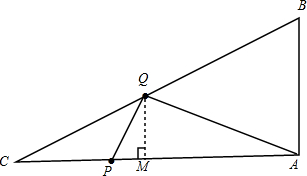

如图所示，过点Q作QM⊥AC，垂足为M，
则CQ=3-$\sqrt{3}$x，
∵在△ABC中，∠A=90°，∠C=30°，
∴QM=$\frac{1}{2}$CQ=$\frac{3-\sqrt{3}x}{2}$，
根据题意，得：$\frac{1}{2}•x•\frac{3-\sqrt{3}x}{2}=\frac{3\sqrt{3}}{16}$，
解得：x=$\frac{\sqrt{3}}{2}$（符合题意）．
答：当AP为$\frac{\sqrt{3}}{2}$时，△APQ的面积为$\frac{3\sqrt{3}}{16}$．

点评 本题主要考查点的运动综合问题，求AP的值分情况讨论是前提，求出高并根据面积列出方程求解是关键．