
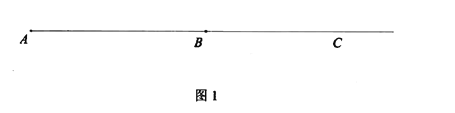
【题目】如图1,点![]() 为线段
为线段![]() 延长线上的一点,点
延长线上的一点,点![]() 是
是![]() 的中点,且点
的中点,且点![]() 不与点
不与点![]() 重合,
重合,![]() ,设
,设![]() .
.
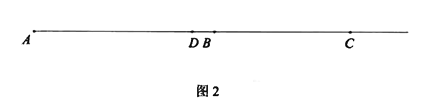
![]() ①若
①若![]() ,如图2,则
,如图2,则![]() ;
;
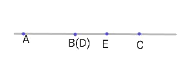
②用含![]() 的代数式表示
的代数式表示![]() 的长,直接写出答案;
的长,直接写出答案; ![]() ,
,![]() ;
;
![]() 若点
若点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,你能说明点
,你能说明点![]() 是线段
是线段![]() 的中点吗?
的中点吗?
【答案】(1)①1;②![]() ;(2)E为BC的中点,详情见解析;
;(2)E为BC的中点,详情见解析;
【解析】
(1)①先求出AC=AB+BC,因为D是AC中点,可求AD,最后由BD=AB-AD进行计算即可;②分类讨论,当点D在AB之间,因为AC=AB+BC=8+x,D是AC中点,所以![]() ,所以
,所以![]() ;当D和B点重合,所以B是AC中点,可得
;当D和B点重合,所以B是AC中点,可得![]() ,
,![]() ;当D在AB之外,因为
;当D在AB之外,因为![]() ,D是AC中点,所以
,D是AC中点,所以![]() ,所以
,所以![]() ;结合三种情况可得
;结合三种情况可得![]() ;
;![]()
(2)分类讨论①当x<8,D在AB上,②当x=8时,AB=BC=8,③当x>8时,D在BC上,由(1)可知,CD=4+![]() x,所以CE=CD-DE=(4+
x,所以CE=CD-DE=(4+![]() x)-4=
x)-4=![]() x,所以CE=
x,所以CE=![]() BC,所以E为BC的中点;
BC,所以E为BC的中点;
解:
(1)①若x=6,则AC=AB+BC=14,
∴D是AC中点,
∴![]() ,
,
∴![]() ,
,
故答案为:1;
②当x<8时,D在AB上,如图,

∵AC=AB+BC=8+x,
又∵D是AC中点,
∴![]() ,
,
∴![]() ,
,
当x=8时,AB=BC=8,如图,

∴B是AC中点,
∴此时B、D重合,
∴![]() ,
,![]() ,
,
当x>8时,D在BC上,如图,
![]()
∵![]() ,
,
又因为D是AC中点,
∴![]() ,
,
∴![]() ,
,
故![]() ;
;![]()
(2)①当x<8,D在AB上,如图,

由(1)可知,CD=4+![]() x,
x,
∴CE=CD-DE=(4+![]() x)-4=
x)-4=![]() x,
x,
∴CE=![]() BC,
BC,
∴E为BC的中点;
②当x=8时,AB=BC=8,如图,
由(1)可知,CD=4+![]() x,
x,
∴CE=CD-DE=(4+![]() x)-4=
x)-4=![]() x,
x,
∴CE=![]() BC,
BC,
∴E为BC的中点;
③当x>8时,D在BC上,如图,

由(1)可知,CD=4+![]() x,
x,
∴CE=CD-DE=(4+![]() x)-4=
x)-4=![]() x,
x,
∴CE=![]() BC,
BC,
∴E为BC的中点;
综上所述,E为BC的中点;


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E. F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A. C两点同时出发,沿△AFB和△CDE各边匀速运动一周。即点P自A→F→B→A停止,点Q自C→D→E→C停止。在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A. P、C. Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A. P、C. Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:|﹣6|﹣7+(﹣3)
(2)计算:﹣32÷3﹣![]() ×(﹣2)3
×(﹣2)3
(3)化简:2(2x2y+x)﹣3(x2y﹣2x)
(4)解方程:5﹣2x=3(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
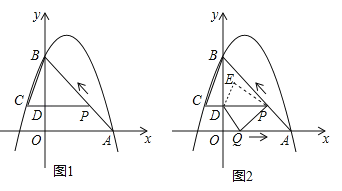
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BD是正方形ABCD的对角线,BC=4,点H是AD边上的一动点,连接CH,作![]() ,使得HE=CH,连接AE。
,使得HE=CH,连接AE。
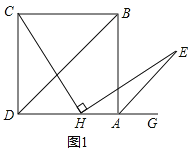

(1)求证:![]() ;
;
(2)如图2,过点E作EF//AD交对角线BD于点F,试探究:在点H的运动过程中,EF的长度是否为一个定值;如果是,请求出EF的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)求证:CP为⊙O的切线;
(2)若BP=1,CP=![]() ,求 ⊙O的半径;
,求 ⊙O的半径;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=![]() ,则称点Q为点P的“可控变点”。例如:点(1,2)的“可控变点”为点(1,2).
,则称点Q为点P的“可控变点”。例如:点(1,2)的“可控变点”为点(1,2).
结合定义,请回答下列问题:

(1)点(3,4)的“可控变点”为点 ___.
(2)若点N(m,2)是函数y=x1图象上点M的“可控变点”,则点M的坐标为___;
(3)点P为直线y=2x2上的动点,当x0时,它的“可控变点”Q所形成的图象如图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点”Q所形成的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大正方形内有两个大小一样的长方形ABCD和长方形EFGH,且AB,AD,EF,EH分别在大正方形的四条边上,大正方形内有个小正方形与两长方形有重叠(图中两个长方形形状的阴影部分),若B两正方形的周长分别为44与30,且AB=EH=6,AD=EF=3,则两阴影部分的周长和为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com