
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 和点
和点![]() ,且
,且![]() ,
,![]() 满足
满足![]() .
.

(1)![]() ______,
______,![]() ______.
______.
(2)点![]() 在直线
在直线![]() 的右侧,且
的右侧,且![]() :
:
①若点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的坐标为______;
的坐标为______;
②若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标.
的坐标.
【答案】(1)-2,4;(2)①![]() ;②点
;②点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)利用非负数的的性质即可求出a,b;
(2)①利用等腰直角三角形的性质即可得出结论;
②分两种情况,利用等腰三角形的性质,及全等三角形的性质求出PC,BC,即可得出结论
解:(1)由题意,得![]() ,
,
所以![]() 且
且![]() ,
,
解得![]() ,
,![]() ;
;
(2)①如图,由(1)知,b=4,
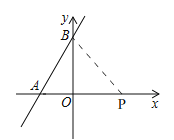
∴B(0,4),
∴OB=4,
点P在直线AB的右侧,且在x轴上,
∵∠APB=45°,
∴OP=OB=4,
∴点![]() 的坐标为
的坐标为![]() .
.
②当![]() 时,过点
时,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
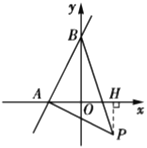
则![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]()
.∴![]() .
.
故点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,作
时,作![]() 轴,
轴,![]() 于点
于点![]() ,
,
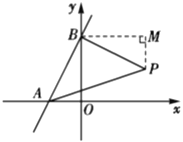
则![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
![]() ,
,![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种空调共50台.已知购进一台甲种空调比购进一台乙种空调进价少0.3万元;用20万元购进甲种空调数量是用40万元购进乙种空调数量的2倍.请解答下列问题:
(1)求甲、乙两种空调每台进价各是多少万元?
(2)若商场预计投入资金不少于10万元,且购进甲种空调至少31台,商场有哪几种购进方案?
(3)在(2)条件下,若甲种空调每台售价1100元,乙种空调每台售价4300元,甲、乙空调各有一台样机按八折出售,其余全部标价售出,商场从销售这50台空调获利中拿出2520元作为员工福利,其余利润恰好又可以购进以上空调共2台.请直接写出该商场购进这50台空调各几台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
已知:如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() 是
是![]() 平分线,交
平分线,交![]() 边于点
边于点![]() .
.

求证:![]() .
.
证明:在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
则由已知条件易知:![]() .
.
∴![]() ,
,
又∵![]() ,∴
,∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ∴
∴![]() .
.
(数学思考)
现将原题中的“![]() 是
是![]() 平分线,交
平分线,交![]() 边于点
边于点![]() ”换成“
”换成“![]() 是
是![]() 的外角平分线,交
的外角平分线,交![]() 边的延长线于点
边的延长线于点![]() ”,如图,其他条件不变,请你猜想线段
”,如图,其他条件不变,请你猜想线段![]() 之间的数量关系,并证明你的猜想.
之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
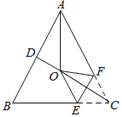
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.小张用骑公共自行车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣2.5 | ﹣2 | ﹣1 | 0 | 0.5 | … |
y | … | ﹣5 | 0 | 4 | 0 | ﹣5 | … |
(1)求二次函数解析式,并写出顶点坐标;
(2)在直角坐标系中画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<﹣1,试比较y1与y2的大小,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,∠B=90°,∠A=30°,AC=4,点E在AC上,AE=3.将三角形纸片按图1方式折叠,使点A的对应点![]() 落在AB的延长线上,折痕为ED,
落在AB的延长线上,折痕为ED,![]() 交BC于点F.
交BC于点F.
(1)求∠CFE的度数;
(2)如图2,,继续将纸片沿BF折叠,点![]() 的对应点为
的对应点为![]() ,
,![]() 交DE于点G .求线段DG的长.
交DE于点G .求线段DG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com