
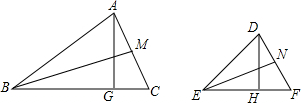
分析 由△ABC∽△DEF可知∠ABG=∠DEH,然后由高线的定义可知∠AGB=∠DHE,从可证明△ABG∽△DEH,于是得到;$\frac{AG}{DH}=\frac{AB}{ED}$,由△ABC∽△DEF可知∠BAM=∠EDN,$\frac{AB}{AC}=\frac{ED}{DF}$,由中线的定义可知$\frac{AM}{DN}=\frac{\frac{1}{2}AC}{\frac{1}{2}DF}=\frac{AC}{DF}$,故此可证明△ABM∽△DEN,从而得到$\frac{BM}{EN}=\frac{AB}{ED}$,于是得到$\frac{AG}{DH}=\frac{BM}{EN}$,整理得:AG•EN=BM•DH.
解答 解:∵△ABC∽△DEF,
∴∠ABG=∠DEH.
∵AG为△ABC的高,DH为△DEF的高,
∴∠AGB=∠DHE=90°.
∴△ABG∽△DEH.
∴$\frac{AG}{DH}=\frac{AB}{ED}$.
∵△ABC∽△DEF,
∴∠BAM=∠EDN,$\frac{AB}{AC}=\frac{ED}{DF}$.
∵BM、EN分别是三角形的中线,
∴AM=$\frac{1}{2}AC$,DN=$\frac{1}{2}DF$.
∴$\frac{AM}{DN}=\frac{AC}{DF}$.
∴△ABM∽△DEN.
∴$\frac{BM}{EN}=\frac{AB}{ED}$.
∴$\frac{AG}{DH}=\frac{BM}{EN}$.
∴AG•EN=BM•DH.
点评 本题主要考查的是相似三角形的性质和判定,证得△ABG∽△DEH、△ABM∽△DEN是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
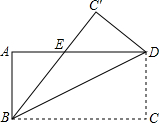 如图,把矩形ABCD沿直线BD向上折叠,使点C落在C′的位置上,已知AB=3,BC=7,重合部分△EBD的面积为$\frac{87}{14}$.
如图,把矩形ABCD沿直线BD向上折叠,使点C落在C′的位置上,已知AB=3,BC=7,重合部分△EBD的面积为$\frac{87}{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
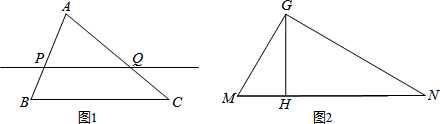
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
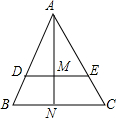 如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.
如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
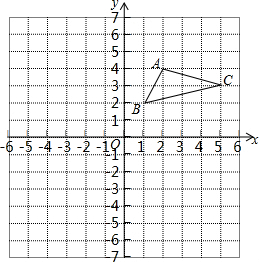 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
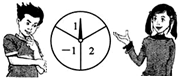 如图,一转盘被等分成三个扇形,上面分别标有-1,2,指针位置固定,转动转盘后任其自由停止后,某个扇形会恰好停在指针所指的位置,得到这个扇形上相应的数.若指针恰好指在等分线上,则需重新转动转盘.
如图,一转盘被等分成三个扇形,上面分别标有-1,2,指针位置固定,转动转盘后任其自由停止后,某个扇形会恰好停在指针所指的位置,得到这个扇形上相应的数.若指针恰好指在等分线上,则需重新转动转盘.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com