
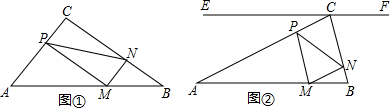
分析 (1)由在Rt△ABC中,∠C=90°,AC=3,AB=5,可求得BC的长,继而求得△ABC的面积,又由MP∥BC,可得△AMP∽△ABC,利用相似三角形的面积比等于相似比的平方,即可求得△AMP的面积.
(2)由MP∥BC,易得△AMP是直角三角形,利用三角函数的知识即可表示出PM与AP,易证得四边形PMNC是矩形,可由S=$\frac{1}{2}$PM•PC,利用二次函数的最值,求得答案.
(3)由MP∥BC,MN∥AC,可得△AMP∽△ABC,△MBN∽△ABC,然后由相似三角形面积比等于相似比的平方,求得S△AMP=$\frac{6}{25}$x2,S△MBN=$\frac{6}{25}$(5-x)2,又由四边形PMNC是平行四边形,可得S=$\frac{1}{2}$[S△ABC-S△AMP-S△MBN],继而求得答案.
解答 解:(1)∵在Rt△ABC中,∠C=90°,AC=3,AB=5,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×3×4=6,
∵MP∥BC,
∴△AMP∽△ABC,
∴$\frac{{S}_{△AMP}}{{S}_{△ABC}}$=($\frac{AM}{AB}$)2=($\frac{1}{5}$)2=$\frac{1}{25}$,
∴S△AMP=$\frac{6}{25}$;
(2)∵MP∥BC,
∴∠APM=∠C=90°,
∴在Rt△AMP中,PM=AM•sinA=$\frac{4}{5}$x,AP=AM•cosA=$\frac{3}{5}$x,
∴PC=AC-AP=3-$\frac{3}{5}$x,
∵MN∥AC,MP∥BC,
∴四边形PMNC是平行四边形,
∵∠C=90°,
∴四边形PMNC是矩形,
∴S=$\frac{1}{2}$PM•PC=$\frac{1}{2}$•$\frac{4}{5}$x•(3-$\frac{3}{5}$x)=-$\frac{6}{25}$x2+$\frac{6}{5}$x=-$\frac{6}{25}$(x-$\frac{5}{2}$)2+$\frac{3}{2}$,
∴S有最大值,最大值为:$\frac{3}{2}$;
(3)有最大值.
∵MP∥BC,MN∥AC,
∴△AMP∽△ABC,△MBN∽△ABC,
∴$\frac{{S}_{△AMP}}{{S}_{△ABC}}$=($\frac{x}{5}$)2,$\frac{{S}_{△MBN}}{{S}_{△ABC}}$=($\frac{5-x}{5}$)2,
∴S△AMP=$\frac{6}{25}$x2,S△MBN=$\frac{6}{25}$(5-x)2,
∵四边形PMNC是平行四边形,
∴S=$\frac{1}{2}$[S△ABC-S△AMP-S△MBN]=$\frac{1}{2}$[6-$\frac{6}{25}$x2-$\frac{6}{25}$(5-x)2]
=-$\frac{6}{25}$x2+$\frac{6}{5}$x=-$\frac{6}{25}$(x-$\frac{5}{2}$)2+$\frac{3}{2}$,
∴S有最大值,最大值为:$\frac{3}{2}$.
点评 此题属于相似三角形的综合题.考查了相似三角形的判定与性质、平行四边形的判定与性质、矩形的判定与性质以及二次函数的最值问题.注意利用二次函数的最值求解是关键.


科目:初中数学 来源: 题型:解答题
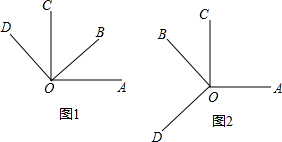 如图1,∠AOC与∠BOD都是直角,∠BOC=50°.
如图1,∠AOC与∠BOD都是直角,∠BOC=50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.
我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
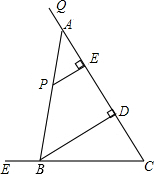 如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
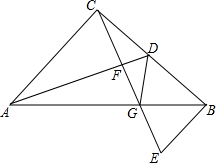 如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.
如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
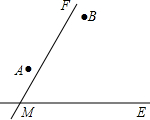 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com