
分析 先根据题意画出图形,然后依据线段中点的定义可知:ME=$\frac{1}{2}AM$,MF=$\frac{1}{2}BM$,从而可得到EF=$\frac{1}{2}AB$.
解答 解:如图所示: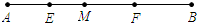
∵E是AM的中点,
∴EM=$\frac{1}{2}AM$.
∵F是MB的中点,
∴MF=$\frac{1}{2}BM$.
∴EF=EM+MF=$\frac{1}{2}(AM+MB)$=$\frac{1}{2}AB$=$\frac{1}{2}a$.
∵EF的长度=$\frac{1}{2}AB$,
∴EF的长与点M的位置无关.
点评 本题主要考查的是两点间的距离,掌握线段中点的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
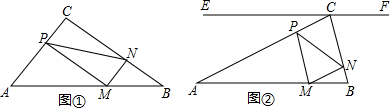
 如图,△ABC中,∠BAC=90°,D是AC上的一点,DE⊥BC于点E,且AD=DE,AE与BD相交于点F.
如图,△ABC中,∠BAC=90°,D是AC上的一点,DE⊥BC于点E,且AD=DE,AE与BD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
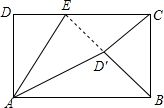 如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.
如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=3x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=ax2+bx+c的图象经过点A,B,C,且点C的坐标为(3,0).
如图,一次函数y=3x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=ax2+bx+c的图象经过点A,B,C,且点C的坐标为(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com