
 如图,一次函数y=3x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=ax2+bx+c的图象经过点A,B,C,且点C的坐标为(3,0).
如图,一次函数y=3x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=ax2+bx+c的图象经过点A,B,C,且点C的坐标为(3,0).分析 (1)由直线y=3x+3交x轴于A点,交y轴于B点,即可求得点A与B的坐标,又由过A、B两点的抛物线交x轴于另一点C(3,0),利用两点式法即可求得抛物线的解析式;
(2)分别从AB=BQ,AQ=BQ,AB=AQ三方面去分析,注意抓住线段的求解方法,借助于方程求解即可求得答案.
解答 解:(1)∵当x=0时,y=3,
当y=0时,x=-1,
∴A(-1,0),B(0,3),
∵C(3,0),
设抛物线的解析式为y=a(x+1)(x-3),
∴3=a×1×(-3),
∴a=-1,
∴此抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3;
(2)存在.
∵抛物线的对称轴为:直线x=$\frac{-1+3}{2}$=1,
∴如图对称轴与x轴的交点即为Q1,
∵OA=OQ1,BO⊥AQ1,
∴当Q1B=AB时,设Q(1,q),
∴1+(q-3)2=10,
∴q=0,或q=6,
∴Q(1,0)或Q(1,6)(在直线AB上,舍去).
当Q2A=Q2B时,设Q2的坐标为(1,m),∴22+m2=12+(3-m)2,
∴m=1,
∴Q2(1,1);
当Q3A=AB时,设Q3(1,n),
∴22+n2=12+32,
∴n=±$\sqrt{6}$,
∴Q3(1,$\sqrt{6}$),Q4(1,-$\sqrt{6}$).
∴符合条件的Q点坐标为Q1(1,0),Q2(1,1),Q3(1,$\sqrt{6}$),Q4(1,-$\sqrt{6}$).
点评 此题考查了待定系数法求二次函数的解析式与等腰三角形的性质等知识.此题难度适中,注意分类讨论思想,方程思想与数形结合思想的应用是解此题的关键,还要注意别漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
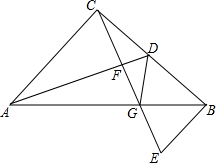 如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.
如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
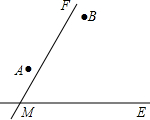 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
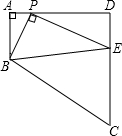 如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.
已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com