
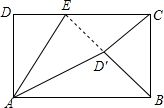
 如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.
如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$. 分析 连接DD′,利用折叠得出AD=AD′,利用矩形的性质,以及△BCD′为等腰三角形,需要分类讨论;进一步求得结论即可.
解答 解:①:CD'=BD'时,如图,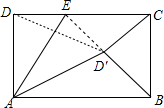
由折叠性质,得AD=AD′,∠DAE=∠D′AE,
∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°,
∵△BCD′为等腰三角形,
∴D′B=D′C,∠D′BC=∠D′CB,
∴∠DCD′=∠ABD′,
在△DD′C和△AD′B中,
$\left\{\begin{array}{l}{DC=AB}\\{∠DCD′=∠ABD′}\\{CD′=BD′}\end{array}\right.$,
∴△DD′C≌△AD′B,
∴DD′=AD′,
∴DD′=AD′=AD,
∴△ADD′是等边三角形,
∴∠DAD′=60°,
∴∠DAE=30°,
∴DE=$\frac{1}{2}$AE,
设DE=x,则AE=2x,
(2x)2-x2=42,
解得:x=$\frac{4}{3}$$\sqrt{3}$,
即DE=$\frac{4}{3}$$\sqrt{3}$.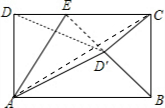 ②:当CD'=CB时,如图,连接AC,
②:当CD'=CB时,如图,连接AC,
由于AD'=4,CD'=4,
而AC=$\sqrt{{7}^{2}+{4}^{2}}$=$\sqrt{65}$>4+4;
故这种情况不存在.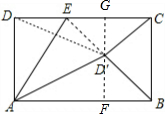 ③当BD'=BC时,如图过D'作AB的垂线,垂足为F,延长D'F交CD于G,
③当BD'=BC时,如图过D'作AB的垂线,垂足为F,延长D'F交CD于G,
由于AD'=BD',D'F=D'F;易知AF=BF,
从而由勾股定理求得D'F=$\sqrt{AD{'}^{2}-A{F}^{2}}$=$\sqrt{{4}^{2}-(\frac{7}{2})^{2}}$=$\frac{\sqrt{15}}{2}$,
又易证△AD'F∽△D'EG,设DE=x,D'E=x,
∴$\frac{D'E}{AD'}=\frac{D'G}{AF}$,即$\frac{x}{4}=\frac{4-\frac{\sqrt{15}}{2}}{\frac{7}{2}}$;
解得x=$\frac{32-4\sqrt{15}}{7}$
综上,故答案为:$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.
点评 此题考查翻折变换,矩形的性质,三角形全等的判定与性质,等腰三角形的性质,勾股定理,掌握折叠的性质,证得三角形全等是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
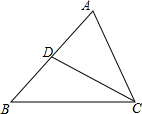 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=2,AC=$\sqrt{5}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=2,AC=$\sqrt{5}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
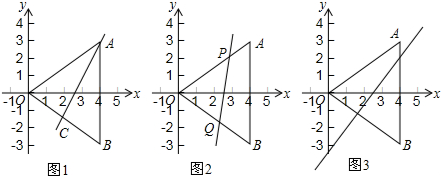
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
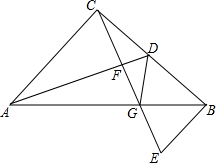 如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.
如图所示,△ABC是等腰直角三角形,CA=CB,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,垂足为F,交AB于点G,过点B作BE⊥BC,交CG的延长线于点E,连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
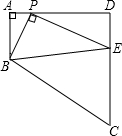 如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com