
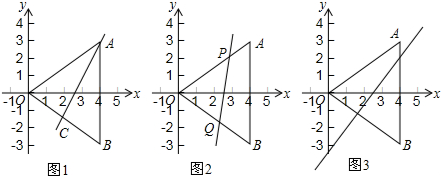
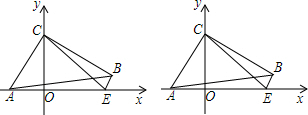
分析 (1)根据直线AC平分△AOB的面积,那么S△AOC=SABC,再由两个三角形高相等可得OC=BC,再根据OA≠AB即可得出结论;
(2)先利用待定系数法求出直线OA与OB的解析式,设点P(4t,3t),则OP=5t,根据直线PQ为△AOB的“等周线”可得出OQ=8-5t,故可用t表示出Q点的坐标,进而可得出结论;
(3)①设N(4,k),则NB=k+3,由直线MN为△AOB的“等周线”可得出MB与OM的长,设M($\frac{4}{5}$k,-$\frac{3}{5}$k),可得出S△AOB=12,由直线MN为△AOB的“等积线”可得出S△MNB=6,由此可得出k的值,进而可得出结论;
②根据①中的结论可画出既是△AOB的“等积线”,又是“等周线”的直线.
解答 解:(1)不存在.
若直线AC平分△AOB的面积,那么S△AOC=SABC,
∵两个三角形高相等,
∴OC=BC.
∵AO≠AB,
∴AO+OC≠BC+BA
∴不存在.
(2)设直线OA的解析式为y=kx(k≠0),
∵A(4,3),
∴4k=3,解得k=$\frac{3}{4}$,
∴直线OA的解析式为y=$\frac{3}{4}$x.
同理可得,直线OB的解析式为y=-$\frac{3}{4}$x.
设点P(4t,3t),则OP=5t,
∵直线PQ为△AOB的“等周线”,
∴OQ=8-5t,
∴Q($\frac{32}{5}$-4t,-$\frac{24}{5}$+3t),
从而|yP-yQ|=$\frac{24}{5}$;
(3)①设N(4,k),则NB=k+3,
∵直线MN为△AOB的“等周线”,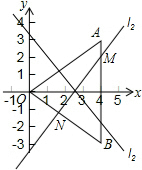
∴MB=8-(k+3)=5-k,
∴OM=OB-MB=k.
设M($\frac{4}{5}$k,-$\frac{3}{5}$k)
∵S△AOB=12,直线MN为△AOB的“等积线”,
∴S△MNB=6,
∴$\frac{1}{2}$(k+3)(4-$\frac{4}{5}$k)=6,
解得k1=2,k2=0,
∴OM=2或OM=0;
②如图所示,共有三条既是△AOB 的“等积线”,又是“等周线”的直线,它们分别是l1、l2和x轴.
点评 本题考查的是一次函数综合题,涉及到用待定系数法求一次函数的解析式及三角形的面积等知识,此题属新定义型题目,正确理解“等积线”和“等周线”的定义是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
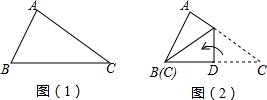
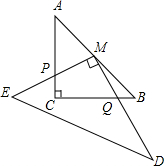 把一块直角三角板DEM的直角顶点M放在等腰的直角三角板ABC的斜边AB的中点M上,ME和MD分别交边AC、BC于点P、Q,求证:MP=MQ.
把一块直角三角板DEM的直角顶点M放在等腰的直角三角板ABC的斜边AB的中点M上,ME和MD分别交边AC、BC于点P、Q,求证:MP=MQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
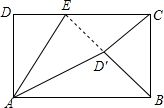 如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.
如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
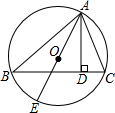 如图所示,△ABC内接于⊙O,AD⊥BC于点D,AE是⊙O的直径.
如图所示,△ABC内接于⊙O,AD⊥BC于点D,AE是⊙O的直径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com