
【题目】如图1,AB⊥BC,分别过点A,C作BM的垂线,垂足分别为M,N.
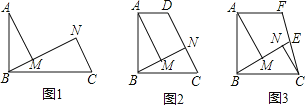
(1)求证:BMBC=ABCN;
(2)若AB=BC.
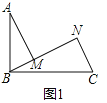
①如图2,若BM=MN,过点A作AD∥BC交CM的延长线于点D,求DN:CN的值;
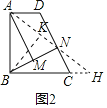
②如图3,若BM>MN,延长BN至点E,使BM=ME,过点A作AF∥BC交CE的延长线于点F,若E是CF的中点,且CN=1,直接写出线段AF的长.
【答案】(1)见解析;(2)①DN:CN=![]() ;②AF=2
;②AF=2![]() ﹣2
﹣2
【解析】
(1)根据两角对应相等的两个三角形相似证明即可.
(2)如图2中,连接AN,延长AN交BC的延长线于H,作BK⊥AN于K.,设CN=m,则BM=CN=MN=m,BN=AM=2m,想办法用m表示AN,NH即可解决问题.
(3)如图3中,连接AE,延长AE交BC的延长线于H.△AFE≌△HCE(ASA),推出AE=EH,AF=CH,利用直角三角形斜边中线的性质求出AE,EH,再利用勾股定理求出BH即可解决问题.
解:(1)证明:如图1中,
∵AM⊥BN,CN⊥BN,AB⊥BC,
∴∠AMB=∠N=∠ABC=90°,
∴∠A+∠ABM=90°,∠ABM+∠CBN=90°,
∴∠A+∠CBN=90°,
∴△ABM∽△BCN,
∴![]() ,
,
∴BMBC=ABCN.
(2)解:①如图2中,连接AN,延长AN交BC的延长线于H,作BK⊥AN于K.
由(1)可知:△ABM∽△BCN,
∴![]()
∵AB=BC,
∴AM=BN,BM=CN,设CN=m,
∵BM=MN,
∴BM=CN=MN=m,BN=AM=2m,
∵AM⊥BN,BM=MN,
∴![]() ,
,
∵![]() .
.
∴![]() ,
,
∴![]() ,
,
∵∠BAK=∠BAH,∠ABH=∠AKB=90°,
∴△ABK∽△AHB,
∴![]() ,
,
∴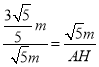 ,
,
∴![]() ,
,
∴![]() ,
,
∵AD∥CH,
∴ .
.
②如图3中,连接AE,延长AE交BC的延长线于H.
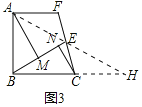
∵AF∥CH,
∴∠F=∠ECH,
∵∠AEF=∠CEH,EF=CF,
∴△AFE≌△HCE(ASA),
∴AE=EH,AF=CH,
∵AM⊥BE,BM=ME,
∴AB=AE,
∵∠ABH=90°,
∴BE=AE=EH,
∵CN=BM=ME=1,
∴BE=AE=EH=2,
∴AB=BC=AE=2,
∴![]() ,
,
∴![]() ,
,
∴AF=2![]() ﹣2.
﹣2.
故答案是:(1)见解析;(2)①DN:CN=![]() ;②AF=2
;②AF=2![]() ﹣2
﹣2


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
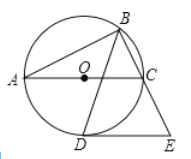
(1)若∠BAC=28°20′,则∠E= ;
(2)求证:DE是⊙O的切线;
(3)若tan∠ACB=2 ,BC=2![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题:
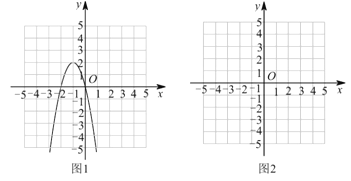
(1)请补全以下求不等式![]() 的解集的过程:
的解集的过程:
①构造函数,画出图象:根据不等式特征构造二次函数![]() ;抛物线的对称轴为_________,开口向下,顶点坐标为__________,与
;抛物线的对称轴为_________,开口向下,顶点坐标为__________,与![]() 轴的交点是_________,用三点法画出二次函数
轴的交点是_________,用三点法画出二次函数![]() 的图象如图1所示;
的图象如图1所示;
②数形结合,求得界点:当![]() 时,求得方程
时,求得方程![]() 的解为___________;
的解为___________;
③借助图象,写出解集:由图象可得不等式![]() 的解集为_________.
的解集为_________.
(2)利用(1)中求不等式解集的方法步骤,求不等式![]() 的解集.
的解集.
①构造函数,画出![]() 的图象(在图2中画出);
的图象(在图2中画出);
②数形结合,求得界点:当![]() __________时,求得方程
__________时,求得方程![]() 的解为__________;
的解为__________;
③借助图象,写出解集.由图2知,不等式![]() 的解集是__________.
的解集是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为一直线上4个点,BC=3,△BCE为等边三角形,⊙O过A,D,E三点,且∠AOD=120°,设AB=x,CD=y,则y与x的函数关系式是( )
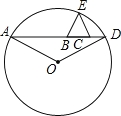
A.y=![]() B.y=
B.y=![]() xC.y=3x+3D.y=
xC.y=3x+3D.y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com