
【题目】如图,在菱形纸片![]() 中,
中,![]() ,将纸片折叠,点
,将纸片折叠,点![]() 分别落在点
分别落在点![]() 处,且
处,且![]() 经过点
经过点![]() 为折痕,当
为折痕,当![]() 时,
时,![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
首先延长DC与AD,交于点M,由四边形ABCD是菱形与折叠的性质,易求得△BCM是等腰三角形,△DFM是含30°角的直角三角形,然后设CF=x,DF=DF=y,利用正切函数的知识,即可求得答案.
解:延长DC与AD,交于点M

∵在菱形纸片ABCD中,∠A=60°
∴∠DCB=∠A=60°
∵AB∥CD
∴∠D=180°-∠A=120°
根据折叠的性质,可得∠ADF=∠D=120°
∴∠FDM=180°-∠ADF=60°
∵DF⊥CD
∴∠DFM=90°,∠M=90°-∠FDM=30°
∵∠BCM=180°-∠BCD=120°
∴∠CBM=180°-∠BCM-∠M=30°
∴∠CBM=∠M=30°
∴BC=CM
设CF=x,DF=DF=y
则BC=CM=CD=CF+DF=x+y
∴FM=CM+CF=2x+y
在Rt△DFM中,tanM=tan30°=![]()
∴x=![]() y
y
∴![]() =
=![]()
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
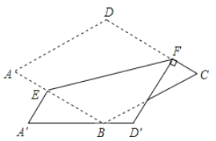
【题目】如图1,AB⊥BC,分别过点A,C作BM的垂线,垂足分别为M,N.
(1)求证:BMBC=ABCN;
(2)若AB=BC.
①如图2,若BM=MN,过点A作AD∥BC交CM的延长线于点D,求DN:CN的值;
②如图3,若BM>MN,延长BN至点E,使BM=ME,过点A作AF∥BC交CE的延长线于点F,若E是CF的中点,且CN=1,直接写出线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
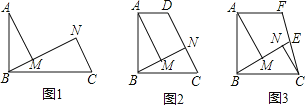
【题目】某学校从甲、乙两名班主任中选拔一名参加教育局组织的班主任技能比赛,选拔内容分案例分析、班会设计、才艺展示三个项目,选拔比赛结束后,统计这两位班主任成绩并制成了如图所示的条形统计图:
(1)乙班班主任三个项目的成绩中位数是 ;
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“80”的概率;
(3)若按照图12所示的权重比进行计算,选拔分数最高的一名班主任参加比赛,应确定哪名班主任获得参赛资格,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
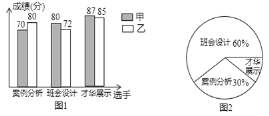
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(本题参考数据:sin67.4°=![]() ,cos67.4°=
,cos67.4°=![]() ,tan67.4°=
,tan67.4°=![]() )
)
(1)求弦BC的长;
(2)请判断点A和圆的位置关系,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
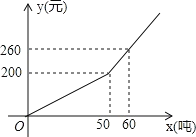
【题目】已知某市2018年企业每月用水量![]() (吨)与该月应缴的水费
(吨)与该月应缴的水费![]() (元)之间的函数关系如图.
(元)之间的函数关系如图.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若某企业2018年10月份的水费为![]() 元,求该企业2018年10月份的用水量;
元,求该企业2018年10月份的用水量;
(3)为贯彻省委发展战略,鼓励企业节约用水,该市自2019年1月开始对月用水量超过![]() 吨的企业加收污水处理费,规定:若企业月用水量
吨的企业加收污水处理费,规定:若企业月用水量![]() 超过
超过![]() 吨,则除按2018年收费标准收取水费外,超过
吨,则除按2018年收费标准收取水费外,超过![]() 吨部分每吨另加收
吨部分每吨另加收![]() 元,若某企业2019年3月份的水费和污水处理费共
元,若某企业2019年3月份的水费和污水处理费共![]() 元,求这个企业该月的用水量.
元,求这个企业该月的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
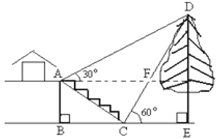
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
查看答案和解析>>
科目:初中数学 来源: 题型:
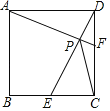
【题目】如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com