
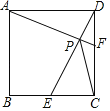
【题目】如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为_____.
【答案】2![]() ﹣2
﹣2
【解析】
根据正方形的性质得到AD=CD=BC=4,∠ADC=∠BCD=90°,求得CE=DF,根据全等三角形的性质得到∠DAF=∠CDE,推出∠APD=90°,得到点P在以AD为直径的圆上,设AD的中点为G,由图形可知:当C、P、G在同一直线上时,CP有最小值,如图所示:根据勾股定理即可得到结论.
解:在正方形ABCD中,AD=CD=BC=4,∠ADC=∠BCD=90°,
∵CE+CF=4,CF+DF=4,
∴CE=DF,
在△ADF和△DCE中,
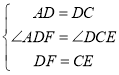 ,
,
∴△ADF≌△DCE(SAS),
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=90°,
∴∠DAP+∠FDP=90°,
∴∠APD=90°,
∴点P在以AD为直径的圆上,
设AD的中点为G,
由图形可知:当C、P、G在同一直线上时,CP有最小值,如图所示:
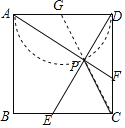
∵CD=4,DG=2,
∴CG=![]() =2
=2![]()
∴CP=CG﹣PG=2![]() ﹣2,
﹣2,
故答案为:2![]() ﹣2.
﹣2.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
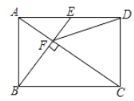
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF.其中正确的结论有( )个
S△ABF.其中正确的结论有( )个
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
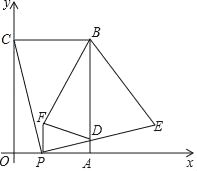
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)直接写出点E的坐标(用含t的代数式表示):_____;
(2)四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;
(3)△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加西部博览会,资阳市计划印制一批宣传册.该宣传册每本共10页,由A、B两种彩页构成.已知A种彩页制版费300元/张,B种彩页制版费200元/张,共计2400元.(注:彩页制版费与印数无关)
(1)每本宣传册A、B两种彩页各有多少张?
(2)据了解,A种彩页印刷费2.5元/张,B种彩页印刷费1.5元/张,这批宣传册的制版费与印刷费的和不超过30900元.如果按到资阳展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率;
(2)用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() 为
为![]() 内一点,将
内一点,将![]() 绕点
绕点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() 得到
得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,且
,且![]() 三点在同一直线上.
三点在同一直线上.
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)如图2,若![]() ,请补全图形,再过点
,请补全图形,再过点![]() 作
作![]() 于点
于点![]() ,然后探究线段
,然后探究线段![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)若![]() ,且点
,且点![]() 满足
满足![]() ,直接写出点
,直接写出点![]() 到
到![]() 的距离.
的距离.
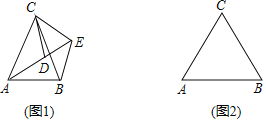
查看答案和解析>>
科目:初中数学 来源: 题型:
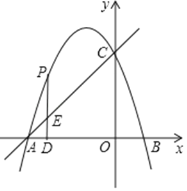
【题目】如图,抛物线y=﹣x2+bx+c与两轴分别交于A、B、C三点,已知点A(﹣3,0),B(1,0).点P在第二象限内的抛物线上运动,作PD⊥x轴于点D,交直线AC于点E.
(1)b= ;c= ;
(2)求线段PE取最大值时点P的坐标,这个最大值是多少;
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,直接写出对应的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
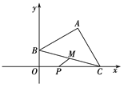
【题目】在平面直角坐标系中,点C、B分别在![]() 轴、
轴、![]() 轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com