
【题目】请完成以下问题: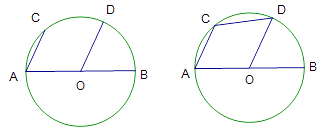
图1 图2
(1)如图1, ![]() ,弦
,弦 ![]() 与半径
与半径 ![]() 平行,求证:
平行,求证: ![]() 是⊙
是⊙ ![]() 的直径;
的直径;
(2)如图2, ![]() 是⊙
是⊙ ![]() 的直径,弦
的直径,弦 ![]() 与半径
与半径 ![]() 平行.已知圆的半径为
平行.已知圆的半径为 ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 与
与 ![]() 的函数关系式.
的函数关系式.
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过对角线BD上点P作直线EF,GH分别平行于AB,BC,那么图中共有( )对面积相等平行四边形.
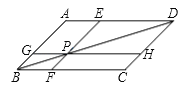
A. 1对B. 2对C. 3对D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为矩形
为矩形![]() 的对角线,将边
的对角线,将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,将边
处,将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处.
处.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 求四边形
求四边形![]() 的面积及
的面积及![]() 与
与![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,tan∠C= ![]() ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A,B的坐标分别为(﹣6,0),(4,0),点D在y轴上.

(1)求点C的坐标;
(2)求对角线AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com