
 如图,二次函数y=x2-4x+3与坐标轴交于A、B、C三点,C点关于对称轴的对称点为D点,点P在抛物线上,且∠PDB=45°,求P点坐标.
如图,二次函数y=x2-4x+3与坐标轴交于A、B、C三点,C点关于对称轴的对称点为D点,点P在抛物线上,且∠PDB=45°,求P点坐标. 分析 连结CD、BC,BC交PD于Q,作QH⊥x轴于H,如图,通过解方程x2-4x+3=0得到A(1,0),B(3,0),则抛物线的对称轴为直线x=2,再确定C(0,3)D(4,3),利用两点间的距离公式计算出BD=$\sqrt{10}$,接着判定△OBC为等腰直角三角形得到BC=3$\sqrt{2}$,∠OCB=∠OBC=45°,然后证明△BDQ∽△BCD,利用相似比求出BQ=$\frac{5\sqrt{2}}{3}$,则在等腰直角三角形BHQ中,QH=BH=$\frac{\sqrt{2}}{2}$BQ=$\frac{5}{3}$,所以AH=OB-BH=$\frac{4}{3}$,于是得到Q($\frac{4}{3}$,$\frac{5}{3}$),接下来利用待定系数法求出直线DP的解析式为y=$\frac{1}{2}$x+1,最后通过解方程组$\left\{\begin{array}{l}{y={x}^{2}-4x+3}\\{y=\frac{1}{2}x+1}\end{array}\right.$得P点坐标.
解答 解:连结CD、BC,BC交PD于Q,作QH⊥x轴于H,如图,
当y=0时,x2-4x+3=0,解得x1=1,x2=3,则A(1,0),B(3,0),
∴抛物线的对称轴为直线x=2,
当x=0时,y=x2-4x+3=3,则C(0,3),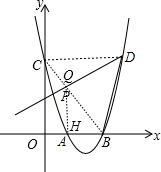
∵C点关于对称轴的对称点为D点,
∴D(4,3),
∴BD=$\sqrt{(4-3)^{2}+{3}^{2}}$=$\sqrt{10}$,
∵OB=OC=3,
∴△OBC为等腰直角三角形,
∴BC=3$\sqrt{2}$,∠OCB=∠OBC=45°,
∴∠BCD=45°,
∵∠PDB=45°,
∴∠BCD=∠BDQ,
而∠QBD=∠DBC,
∴△BDQ∽△BCD,
∴BQ:BD=BD:BC,即BQ:$\sqrt{10}$=$\sqrt{10}$:3$\sqrt{2}$,解得BQ=$\frac{5\sqrt{2}}{3}$,
在等腰直角三角形BHQ中,QH=BH=$\frac{\sqrt{2}}{2}$BQ=$\frac{5}{3}$,
∴AH=OB-BH=3-$\frac{5}{3}$=$\frac{4}{3}$,
∴Q($\frac{4}{3}$,$\frac{5}{3}$),
设直线DP的解析式为y=kx+b,
把D(4,3),Q($\frac{4}{3}$,$\frac{5}{3}$)代入得$\left\{\begin{array}{l}{4k+b=3}\\{\frac{4}{3}k+b=\frac{5}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直线DP的解析式为y=$\frac{1}{2}$x+1,
解方程组$\left\{\begin{array}{l}{y={x}^{2}-4x+3}\\{y=\frac{1}{2}x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{5}{4}}\end{array}\right.$,
∴P点坐标为($\frac{1}{2}$,$\frac{5}{4}$).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了相似三角形的判定与性质.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:选择题
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | -0.01<x<0.02 | B. | 6.17<x<6.18 | C. | 6.18<x<6.19 | D. | 6.19<x<6.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一个棱长为10cm的正方体盒子,现需从底部A点处起,沿盒子的三个表面到顶部的B点处张贴一条彩色纸带(纸带的宽度忽略不计),则所需纸带的最短长度是=10$\sqrt{10}$cm.
如图是一个棱长为10cm的正方体盒子,现需从底部A点处起,沿盒子的三个表面到顶部的B点处张贴一条彩色纸带(纸带的宽度忽略不计),则所需纸带的最短长度是=10$\sqrt{10}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.
如图,在?ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )| A. | 15m | B. | 17m | C. | 20m | D. | 28m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com