
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为
为![]() 上一个动点(不与
上一个动点(不与![]() ,
,![]() )重合),连接
)重合),连接![]() .
.


图1 图2
(1)直接写出![]() ___________,
___________,![]() ___________;
___________;
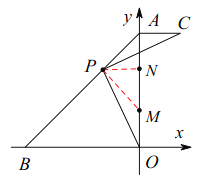
(2)如图1,过点![]() 作
作![]() 的垂线交过点
的垂线交过点![]() 平行于
平行于![]() 轴的直线于点
轴的直线于点![]() ,若点
,若点![]() ,
,
求点![]() 的坐标;
的坐标;
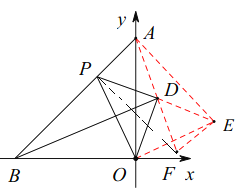
(3)如图2,以![]() 为斜边在
为斜边在![]() 右侧作等腰
右侧作等腰![]() ,
,![]() .连接
.连接![]() ,当点
,当点![]() 从
从![]() 向
向![]() 运动过程中,
运动过程中,![]() 的面积是否发生变化,请判断并说明理由.
的面积是否发生变化,请判断并说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)面积不变为4,理由见解析.
;(3)面积不变为4,理由见解析.
【解析】
(1)根据完全平方公式即可化简,再根据非负性求解;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,证明△APM为等腰直角三角形,再得到
,证明△APM为等腰直角三角形,再得到![]() ,得到
,得到![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,根据
,根据![]() 得到
得到
![]() ,故可得到OM,即可求出AC的长,即可求解;
,故可得到OM,即可求出AC的长,即可求解;
(3)延长![]() 到
到![]() ,使
,使![]() , 得到
, 得到![]() 为等腰三角形,再证明
为等腰三角形,再证明![]() 得到
得到![]() ,根据直角三角形斜边上的中线性质得到AD=PD=DE,延长
,根据直角三角形斜边上的中线性质得到AD=PD=DE,延长![]() 至点
至点![]() ,使
,使![]() ,得到四边形APFE为矩形,得到点
,得到四边形APFE为矩形,得到点![]() 在运动过程中,点
在运动过程中,点![]() 在
在![]() 垂直平分线上运动,可得△BOD的BO边上的高为
垂直平分线上运动,可得△BOD的BO边上的高为![]() ,再根据三角形的面积即可求解.
,再根据三角形的面积即可求解.
(1)∵![]()
![]()
![]()
∴a+b=0,a-4=0,
∴a=4,b=-4
故答案为:![]() ,
,![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,
,
∵A(0,4),B(-4,0)
∴∠BAO=45°,
∴△APM为等腰直角三角形,
∵∠OPC=∠MPA=90°
∴∠OPC-∠MPC=∠MPA-∠MPC
∴∠OPM=∠CPA
∴AP=MP,∠PAM=∠PMA=45°
又∠PAC=∠PMO=135°
∴![]() ,
,
![]() ,
,
过![]() 作
作![]() 轴于点
轴于点![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,
,
∵△POD为等腰直角三角形,
∴PD=OD=DE,OD⊥PE
则![]() 为等腰三角形,
为等腰三角形,
∴PO=EO
∴AO=BO,∠POE=∠AOB=90°,
∵∠POE-∠AOP=∠AOB-∠AOP
∴∠POB=∠EOA
∴![]() (SAS)
(SAS)
![]() ,
,
∴AD=PD=DE,
延长![]() 至点
至点![]() ,使
,使![]() ,
,
∴AD=DF=PD=DE,
∴四边形APFE为矩形,
![]() ,即
,即![]() ,
,
![]() 点
点![]() 在运动过程中,点
在运动过程中,点![]() 在
在![]() 垂直平分线上运动,
垂直平分线上运动,
∴△BOD的BO边上的高为![]() ,
,
![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
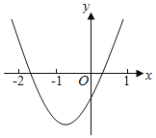
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
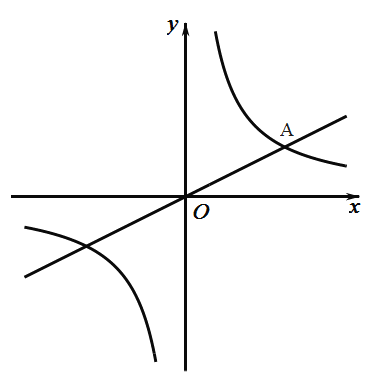
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 在第一象限交于
在第一象限交于![]() 点,且点
点,且点![]() 的横坐标为4,点
的横坐标为4,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的函数解析式;
(2)若点![]() 的纵坐标为8,试判断
的纵坐标为8,试判断![]() 形状,并说明理由.
形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高1元,其每天的销售量就减少20件.
(1)当售价定为12元时,每天可售出________件;
(2)要使每天利润达到640元,则每件售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点P(0,2),以P为圆心,OP为半径的半圆与y轴的另一个交点是C,一次函数![]() (m为实数)的图象为直线l,l分别交x轴,y轴于A,B两点,如图1.
(m为实数)的图象为直线l,l分别交x轴,y轴于A,B两点,如图1.
(1)B点坐标是 (用含m的代数式表示),∠ABO= °.
(2)若点N是直线AB与半圆CO的一个公共点(两个公共点时,N为右侧一点),过点N作⊙P的切线交x轴于点E,如图2.是否存在这样的m的值,使得△EBN是直角三角形.若存在,求出m的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
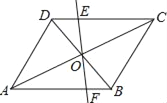
【题目】如图,点O是平行四边形ABCD的对称中心,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F.
(1)证明:△DEO≌△BFO;
(2)若DB=2,AD=1,AB=![]() ,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
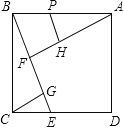
【题目】如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为 _________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com