Question

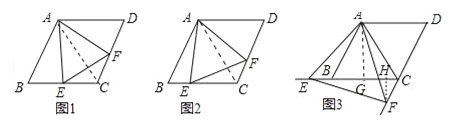
【题目】已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．

（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；

（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；

（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．

Answer 1

【答案】（1）AE=EF=AF；（2）证明见解析；（3）．

【解析】

试题分析：（1）结论AE=EF=AF．只要证明AE=AF即可证明△AEF是等边三角形．

（2）欲证明BE=CF，只要证明△BAE≌△CAF即可．

（3）过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，根据FH=CFcos30°，因为CF=BE，只要求出BE即可解决问题．

试题解析：（1）解：结论AE=EF=AF．

理由：如图1中，连接AC，∵四边形ABCD是菱形，∠B=60°，∴AB=BC=CD=AD，∠B=∠D=60°，∴△ABC，△ADC是等边三角形，∴∠BAC=∠DAC=60°

∵BE=EC，∴∠BAE=∠CAE=30°，AE⊥BC，∵∠EAF=60°，∴∠CAF=∠DAF=30°，∴AF⊥CD，∴AE=AF（菱形的高相等），∴△AEF是等边三角形，∴AE=EF=AF．

（2）证明：如图2中，∵∠BAC=∠EAF=60°，∴∠BAE=∠CAE，在△BAE和△CAF中，∵∠BAE=∠CAF，BA=AC，∠B=∠ACF，∴△BAE≌△CAF，∴BE=CF．

（3）解：过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，∵∠EAB=15°，∠ABC=60°，∴∠AEB=45°，在RT△AGB中，∵∠ABC=60°AB=4，∴BG=2，AG=，在RT△AEG中，∵∠AEG=∠EAG=45°，∴AG=GE=，∴EB=EG﹣BG=，∵△AEB≌△AFC，∴AE=AF，EB=CF=，∠AEB=∠AFC=45°，∵∠EAF=60°，AE=AF，∴△AEF是等边三角形，∴∠AEF=∠AFE=60°

∵∠AEB=45°，∠AEF=60°，∴∠CEF=∠AEF﹣∠AEB=15°，在RT△EFH中，∠CEF=15°，∴∠EFH=75°，∵∠AFE=60°，∴∠AFH=∠EFH﹣∠AFE=15°，∵∠AFC=45°，∠CFH=∠AFC﹣∠AFH=30°，在RT△CHF中，∵∠CFH=30°，CF=，∴FH=CFcos30°==，∴点F到BC的距离为．