
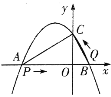
【题目】如图,已知抛物线y=-![]() 与x轴交于A,B两点,与y轴交于点C,其中点A的坐标为(-3,0).
与x轴交于A,B两点,与y轴交于点C,其中点A的坐标为(-3,0).
(1)求b的值及点B的坐标;
(2)试判断△ABC的形状,并说明理由;
(3)一动点P从点A出发,以每秒2个单位的速度向点B运动,同时动点Q从点B出发,以每秒1个单位的速度向点C运动(当点P运动到点B时,点Q随之停止运动),设运动时间为t秒,当t为何值时,△PBQ与△ABC相似?
【答案】(1)![]() ,B的坐标为(1,0);(2)△ABC是直角三角形,理由见解析;(3)当t=1秒或
,B的坐标为(1,0);(2)△ABC是直角三角形,理由见解析;(3)当t=1秒或![]() 秒时,△PBQ与△ABC相似
秒时,△PBQ与△ABC相似
【解析】
(1)将点A的坐标代入![]() 中可解得b的值,由此可得抛物线的解析式,在所得解析式中令y=0得到关于x的方程,解方程即可求得点B的坐标;
中可解得b的值,由此可得抛物线的解析式,在所得解析式中令y=0得到关于x的方程,解方程即可求得点B的坐标;
(2)由(1)中所得抛物线的解析式可求得点C的坐标,结合点A、B的坐标可求得OA、OB、OC和AB的长度,这样由勾股定理可求得AC和BC的长,再证AB2=AC2+BC2可得△ABC是直角三角形;
(3)由题意用含t的代数式表达出BP和BQ的长度,结合∠ABC是公共角,∠ACB=90°,分∠PQB=90°和∠QPB=90°两种情况进行讨论即可求得△PBQ与△ABC相似时对应的t的值.
(1)将点A(-3,0)代入抛物线![]() 可得:
可得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ,
,
令y=0,得![]() ,解得x1=-3, x2=1,
,解得x1=-3, x2=1,
∴点B的坐标为:(1,0);
(2)△ABC是直角三角形,理由如下:
对于抛物线![]() ,令x=0,得y=
,令x=0,得y=![]() ,
,
∴点C的坐标为(0,![]() ),
),
∴OC=![]() ,OA=3,OB=1,AB=4,
,OA=3,OB=1,AB=4,
∴在Rt△AOC中,由勾股定理可得AC=![]() ,在Rt△COB中,由勾股定理可得BC=2,
,在Rt△COB中,由勾股定理可得BC=2,
∴AC2+BC2=12+4=16=AB2,
∴∠ACB=90°,
∴△ABC是直角三角形;
(3)由题意可得:AP=2t,BP=4-2t,BQ=t,CQ=2-t,
∵在△ABC和△PBQ中,∠ABC和∠PBQ是公共角,∠ACB=90°,
∴若△PBQ与△ABC相似,则∠PQB=90°或∠QPB=90°,
①当∠PQB=90°时,易得AC∥PQ,则△PQB~△ACB,
∴ ![]() ,即
,即![]() ,解得t=1;
,解得t=1;
②当∠QPB=90°,则△QPB~△ACB,
∴ ![]() ,即
,即![]() ,解得
,解得![]() ;
;
综上所述:当t=1秒或![]() 秒时,△PBQ与△ABC相似.
秒时,△PBQ与△ABC相似.


科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b与反比例函数y=![]() (x>0)的图像交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C,D两点,则m=________,n=________;若M(x1,y1),N(x2,y2)是反比例函数y=
(x>0)的图像交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C,D两点,则m=________,n=________;若M(x1,y1),N(x2,y2)是反比例函数y=![]() (x>0)的图像上两点,且0<x1<x2,则y1________y2(填“<”“=”或“>”).
(x>0)的图像上两点,且0<x1<x2,则y1________y2(填“<”“=”或“>”).

查看答案和解析>>
科目:初中数学 来源: 题型:
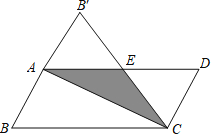
【题目】如图,在平行四边形纸片ABCD中,AB=3cm,将纸片沿对角线AC对折,BC边的对应边B′C与AD边交于点E,此时△CDE恰为等边三角形中,求:
(1)AD的长度.
(2)重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
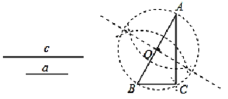
【题目】数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.李明的作法如图所示,作线段AB使AB=C,以AB为直径作⊙O,以B为圆心,a为半径作弧交⊙O于点C,连接AC,△ABC即为所求作的三角形,你认为这种作法中判断∠ACB是直角的依据是( )
A. 90°的圆周角所对的弦是直径 B. 直径所对的圆周角是直角
C. 勾股定理的逆定理 D. 勾股定理
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图将矩形ABCD的四个内角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )

A. 8+6![]() B. 12
B. 12![]() C. 19.2D. 20
C. 19.2D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:

(1)楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
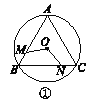
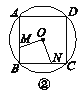
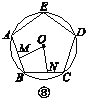
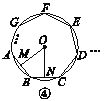
【题目】如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com