Question

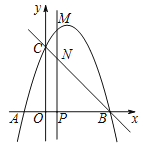
【题目】如图，抛物线与轴交于、两点（点在点的左侧），点的坐标为，与轴交于点，作直线．动点在轴上运动，过点作轴，交抛物线于点，交直线于点，设点的横坐标为．

（Ⅰ）求抛物线的解析式和直线的解析式；

（Ⅱ）当点在线段上运动时，求线段的最大值；

（Ⅲ）当以、、、为顶点的四边形是平行四边形时，直接写出的值．

Answer 1

【答案】（1）y=﹣x2+2x+3，y=﹣x+3；（2）当m=时，MN有最大值，MN的最大值为；（3）或．

【解析】（1）由A、C两点的坐标利用待定系数法可求得抛物线解析式，则可求得B点坐标，再利用待定系数法可求得直线BC的解析式；

（2）用m可分别表示出N、M的坐标，则可表示出MN的长，再利用二次函数的最值可求得MN的最大值；

(3) 由条件可得出MN=OC，结合（2）可得到关于m的方程，可求得m的值

本题解析：

（1）∵抛物线过A、C两点，

∴代入抛物线解析式可得 ，解得，

∴抛物线解析式为y=﹣x2+2x+3，

令y=0可得，﹣x2+2x+3=0，解x1=﹣1，x2=3，

∵B点在A点右侧，

∴B点坐标为（3，0），

设直线BC解析式为y=kx+s，

把B、C坐标代入可得 ，解得 ，

∴直线BC解析式为y=﹣x+3；

（2）∵PM⊥x轴，点P的横坐标为m，

∴M（m，﹣m2+2m+3），N（m，- m+3），

∵P在线段OB上运动，

∴M点在N点上方，

∴MN=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m=﹣（m﹣）2+，

∴当m=时，MN有最大值，MN的最大值为；

（3）∵PM⊥x轴，

∴MN∥OC，

当以C、O、M、N为顶点的四边形是平行四边形时，则有OC=MN，

当点P在线段OB上时，则有MN=﹣m2+3m，

∴﹣m2+3m=3，此方程无实数根，

当点P不在线段OB上时，则有MN=﹣m+3﹣（﹣m2+2m+3）=m2﹣3m，

∴m2﹣3m=3，解得m=或m=，

综上可知当以C、O、M、N为顶点的四边形是平行四边形时，m的值为或．